我们这里主要解读三篇:

因为第二，三篇是基于第一篇的改进，所以我们着重理解第一篇。

AlphaGo Lee

我们之前有讲过MCTS，而AlphaGo Lee这篇论文本质上是在用Neural Network来改进MCTS中的Tree Policy和Rollout Policy。我们也有讲过，围棋的复杂度 $O(W^H)$ 过高是其AI设计难度大的主要原因，而本文从两方面解决这个问题：减少MCTS搜索的广度和深度。

Supervised Learning of Policy Networks

在第一阶段，作者从KGS Go Server上采集了百万级别的棋谱，将其做成数据集以供训练。在训练中，将棋盘信息作为输入，将棋谱的走棋位置作为输出。神经网络的结构其实很简单，类似于VGG的结构，13层CNN，用标准的DL训练方法SGD，test set accuracy达到55.7%；在加了一些feature engineeering之后，test set accuracy达到了57%

作者将训练的SL Policy替换比赛用的SL Policy，与标准比赛版AlphaGo对局，发现准确率的小幅提升，对结果影响巨大。如下图，有意思的是，同等training accuracy下，更小的网络反而会有更高的胜率，只不过小网络的training accuracy的上限更低。

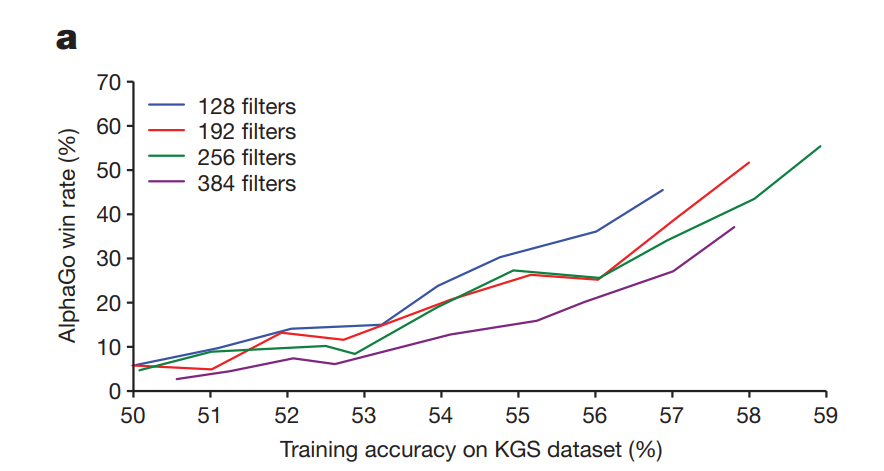
另外，作者还用数据集训练，训练了一个简单的Linear Softmax Network，作为fast rollout policy备用。相比SL Policy，其准确率低到24.2%，但是一步棋仅用 $2\mu s$ ，而SL Policy一步棋要用 $3ms$ 。

第一阶段的SL Policy，是为第二阶段的RL Policy准备的。

Reinforcement Learning of Policy Networks

第二阶段的主要目的，在SL Policy的基础上，提升其准确率，也可以说:

RL policy network finetunes from SL policy network using reinforcement learning.

具体而言，作者用输赢作为奖励信号( $r_t=+1$ as win and $r_t=-1$ as loss)，随机从训练中的checkpoint networks选择一个作为对手与当前训练的network对局，若输则整局的 $r_t=-1$ ，赢则整局 $r_t=+1$ ，用标准的policy gradient更新:

\Delta \rho = \frac{\partial \log p_\rho(a_t|s_t)}{\partial \rho}r_t

这就是媒体所谓的左右互搏。令我感到意外的是，仅仅用从RL policy sample出来的action而不用任何搜索，与最强的MCTS业余二段AI Pachi对阵，即可达到85%的胜率，与之前的SL Policy对阵能达到80%的胜率。

第二阶段的RL Policy，是为第三阶段的RL Value Network做准备的。

Reinforcement Learning for Value Networks

相比于Policy Network预测走棋位置，Value Network预测的是当前局面的胜率。训练的方法很简单，将预测胜率与真实对阵的结果( $z=1$ as win and $z=0$ as loss)的Mean Squre Error作为loss，用SGD训练：

\Delta \theta = \frac{\partial v_\theta(s)}{\partial \theta}(z - v_\theta)

作者发现，仅仅用KGS的dataset已经满足不了庞大的neural network了，training loss和testing loss差距巨大，也就是说DNN overfitting了。

这时，之前训练出来的RL Policy Network就派上用场了，RL Policy自己和自己对阵，产生了30M个棋局，是KGS dataset的数倍之多。用这些self play数据来train value network，overfitting的问题就解决了。

作者比较了value network预测的胜率和几种不同的policy rollout出来的结果，与真实专家棋局数据的胜负的mean square error，如下图：

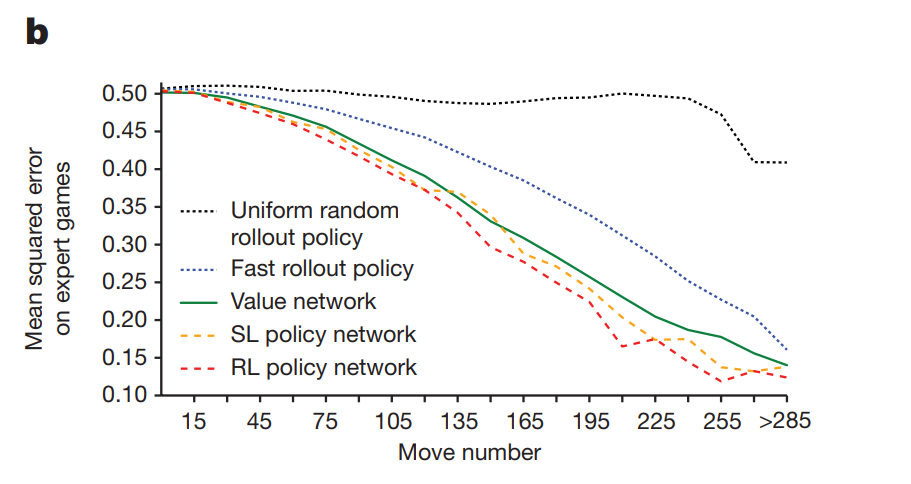
显然RL Policy与专家的棋路最吻合，且残局阶段更容易预测，这都很好理解。

Search with Policy and Value Networks

有了Policy Network和Value Network，将其与MCTS结合，就成了AlphaGo。

AlphaGo的Tree Policy如下：

a = \arg\max_a Q(s,a) + U(s,a) \\U(s,a) \propto \frac{P(s,a)}{1+N(s,a)}

其中 $Q(s,a)$ 我们等下讲， $N(s,a)$ 为该节点的访问次数， $P(s,a)$ 为SL Policy的output probability。作者发现这里用SL Policy的performance好于RL Policy，猜测可能是SL的action更diverse一些。

我们应该记得，MCTS会有一个rollout policy，用来simulate leaf node的胜负。我们在train SL policy的时候，也训练了一个fast rollout policy，其simulate出来的胜负记作 $z_L\in \{0, 1\}$ ，而AlphaGo将value network预测的胜率，与fast rollout policy跑出来的胜负混合:

V(s_L) = (1-\lambda)v_\theta(s_L) + \lambda z_L

以此来计算 $Q(s,a)$ :

Q(s,a) = \frac{1}{N}\sum_i \mathbf{1}(s,a,i)V(s_L^i) \\N(s,a) = \sum_i \mathbf{1}(s,a,i)

其中， $\mathbf{1}(s,a,i)$ 指的是，第 $i$ 次simulation中 $\lt s,a>$ 这个节点，有无被访问过， $V(s_L^i)$ 是第 $i$ 次simuate时用leaf node $s_L$ 的算出来的 $V(s_L)$ 。在实际中，取 $\lambda=0.5$ 作为混合参数。

到这里，AlphaGo基本训练流程已经大致清楚了。更细致的工作在nature文章后面method里面有讲。精秒的设计，详实的数据，漂亮的图表，海量的调参和对比，巨大的计算力，背后惊人的的工程量，初次拜读时，让我对这篇文章叹为观止，这种佳作，一般的ML Conference or Journal确实配不上这篇文章。

AlphaGo Zero

有了AlphaGo Lee的成功，对其细节的改进是自然而然的事情。本作做了以下两点改进：网络结构和训练流程。

Network Architecture

这部分很简单。一是将网络结构从13-layer VGG调整为40 blocks ResNet，因为2015年前AlphaGo Lee研发时ResNet等更好的网络结构还未出现；二是Policy Network和Value Network共享Network Body但有Seperated Head，这点和DL里的Multi-task的思路差不多。总之，这部分的改进来自于DL社区的进步。下图讨论了网络结构对performance的贡献，影响还蛮大的。

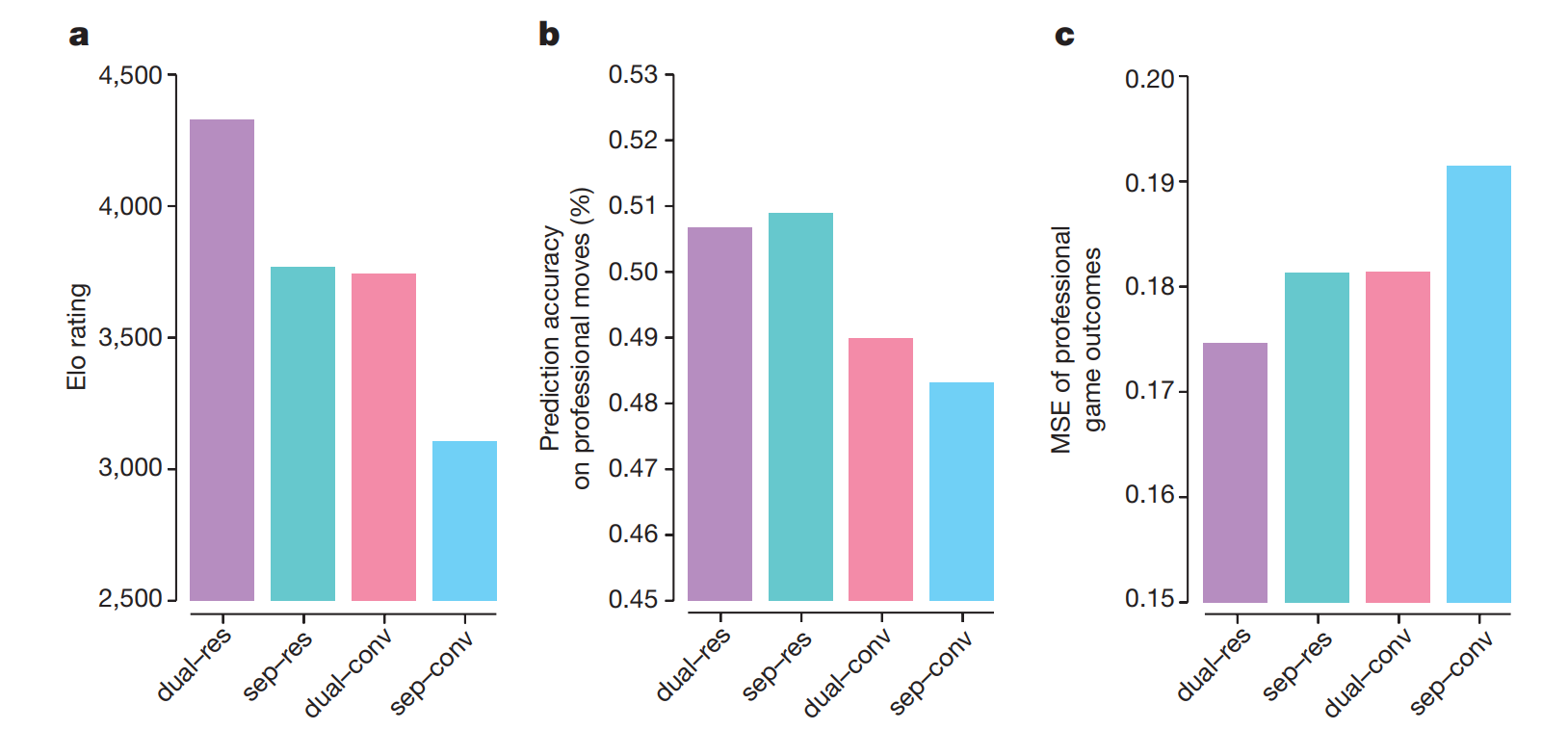
Training Pipeline

AlphaGo Lee的AI训练分了好几步，相比之下，AlphaGo Zero的训练就简单多了。AlphaGo Zero没有用任何人类的棋谱数据库，所有的训练数据都是自己产生的。在一开始，网络参数是随机初始化的；Self-play的过程中，每一步走棋都用MCTS搜索的结果并记录；完成整场游戏后，再开始训练网络更新参数；如下图。

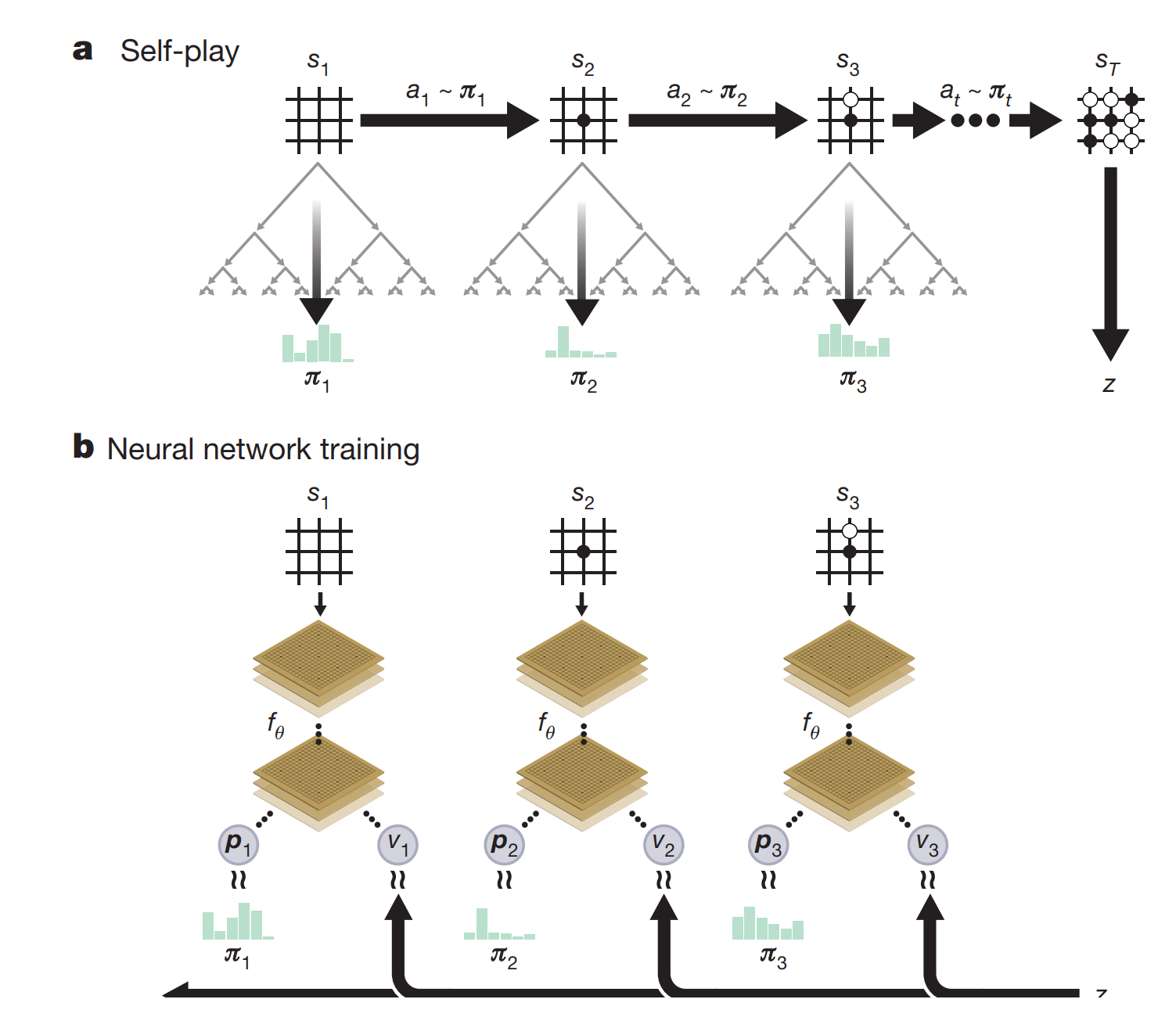
更新网络时loss的计算如下：

L(\theta) = (z - v)^2 - \pi^T \log p + c\| \theta \|^2

要理解上式中的每个参数，我们需要再解释下AlphaGo的MCTS的搜索过程。AlphaGo Zero的MCTS的每一次simualtion都有三步：Selection, Expand & Evaluate, Backup。如下图：

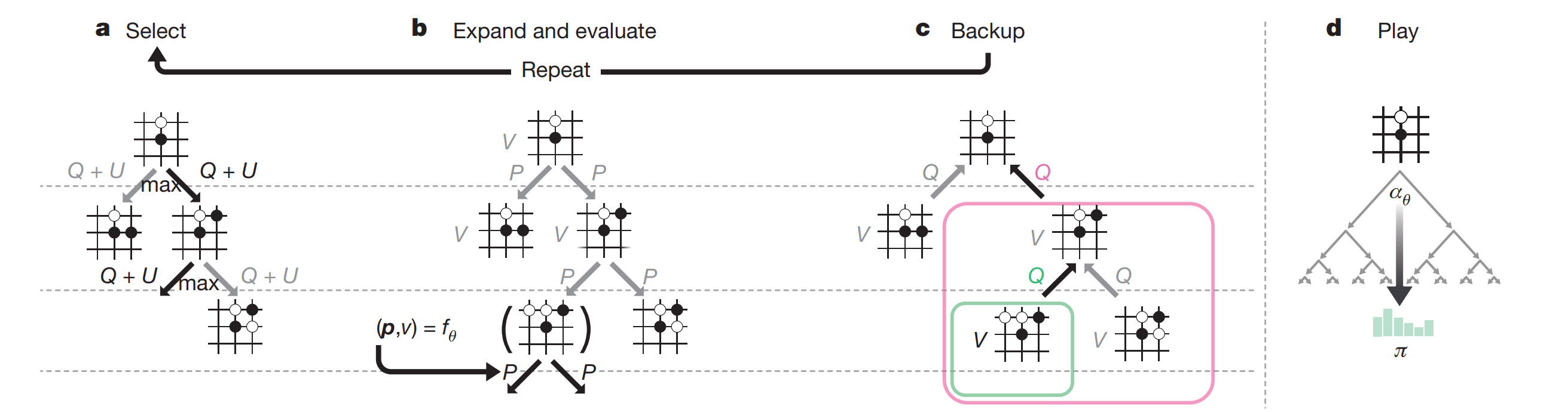
这里，我们需要记录以下几个参数：

$N(s,a)$ : visit count
$W(s,a)$ : accumulated action value
$Q(s,a)$ : average action value
$P(s,a)$ : prior probability of selected edge

在Select的阶段：

a = \arg\max_a Q(s, a) + U(s, a)

其中

U(s, a) = c_{p} P(s,a) \frac{\sqrt{\sum_b N(s,b)}}{1 + N(s,a)}

我们解释下 $U(s, a)$ ，这是所谓的variant of PUCT，其中 $P(s,a)$ 是network的policy head的输出值， $\sum_b N(s,b)$ 是 $s$ 的所有子节点访问次数之和； $c_p$ 控制着exploration，这点在MCTS里讲过。

在Expand & Evalute阶段，记录leaf node的节点 $s_L$ 对应的network的value head的输出值 $v(s_L)$ ，相比于AlphaGo Lee，这里没有用default policy去simulate到游戏结束，节省了大笔时间。

在Backup阶段，沿着leaf node往上到root node的所有节点更新如下：

N(s, a) = N(s, a) + 1 \\W(s, a) = W(s, a) + v(s_L) \\Q(s, a) = W(s, a) / N(s, a)

一个Select - Expand & Evaluate - Backup循环算一个simulation。MCTS每走一步棋前，要执行1600次的simulation，耗时大约0.4秒。

在走棋时，我们用MCTS对根节点 $s_0$ 搜索的结果：

a \sim \pi(a|s_0) = \frac{N(s_0,a)^{1/\tau}}{\sum_b N(s_0,b)^{1/\tau}}

其中 $\tau$ 控制着走棋的exploration temperature，刚开始时 $\tau = 1$ 增加走棋的diversity；后来逐渐降温 $\tau \rightarrow 0$ ，选择访问次数最多的子节点。

走完若干盘棋后，开始训练。这时候回来看loss function就很简单了：

L(\theta) = (z - v)^2 - \pi^T \log p + c\| \theta \|^2

$z \in \{-1, 1\}$ 是整盘棋的最终胜负结果
$\langle p, v \rangle = f_\theta(s)$ 中， $v$ 是network对当前棋局的evaluation，即value head的输出scalar; $p$ 是policy head输出的action probability vector
$\pi$ 是MCTS阶段的走棋策略
$\theta$ 是网络参数

如此，loss第一项是预测胜率与实际胜负的MSE，第二项是MCTS的走棋策略和网络输出的policy的cross entropy，第三项是网络参数的regularization。

Performance

新的算法，运行时不仅需要更少的计算资源，而且带来更好的performance。如下图

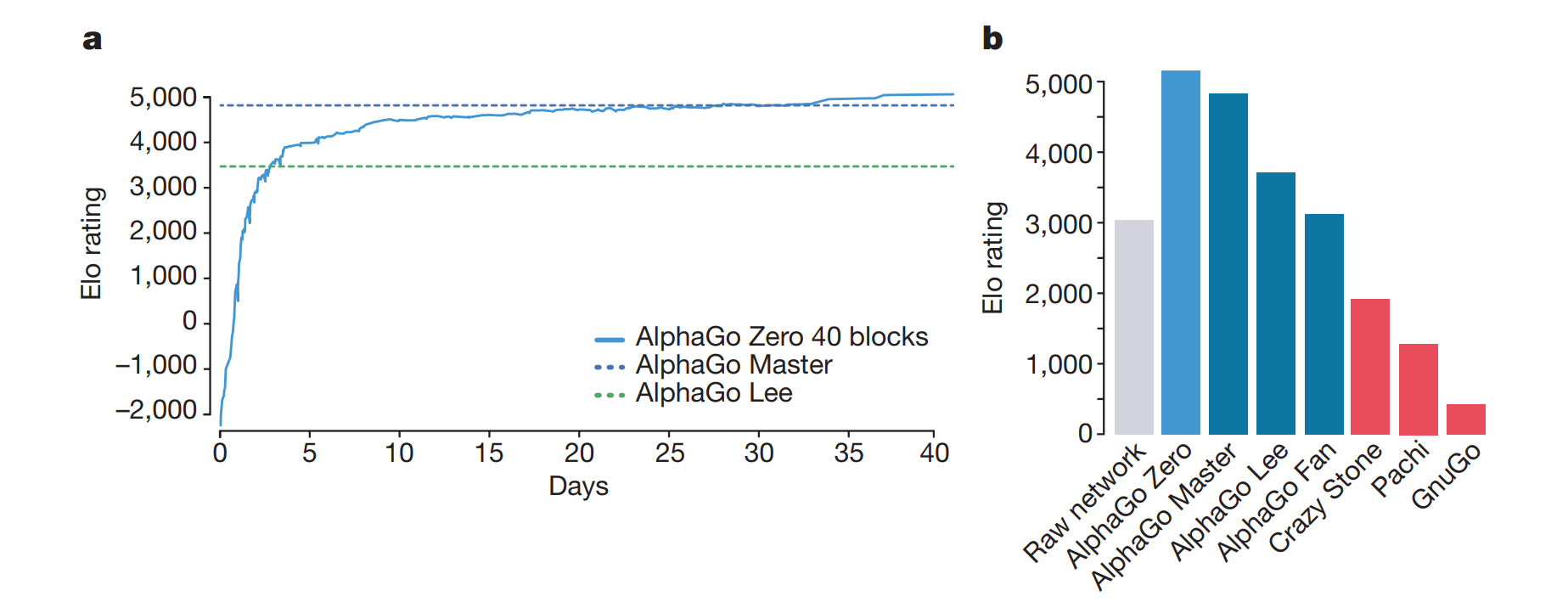
AlphaGo Master算法与AlphaGo Zero一样，但是用了输入用了额外的handcrafted feature，且网络初始值从human data里训练的得来。AlphaGo Lee运行时需要48个TPU，而AlphaGo Zero仅仅用了4个TPU。

MuZero

MuZero在AlphaGo Zero的基础上增加了model-based reinforcement learning的部分，而其他部分与AlphaGo Zero一模一样，另外增加了其他游戏的实验，所以我们就着下图简单解释一下。

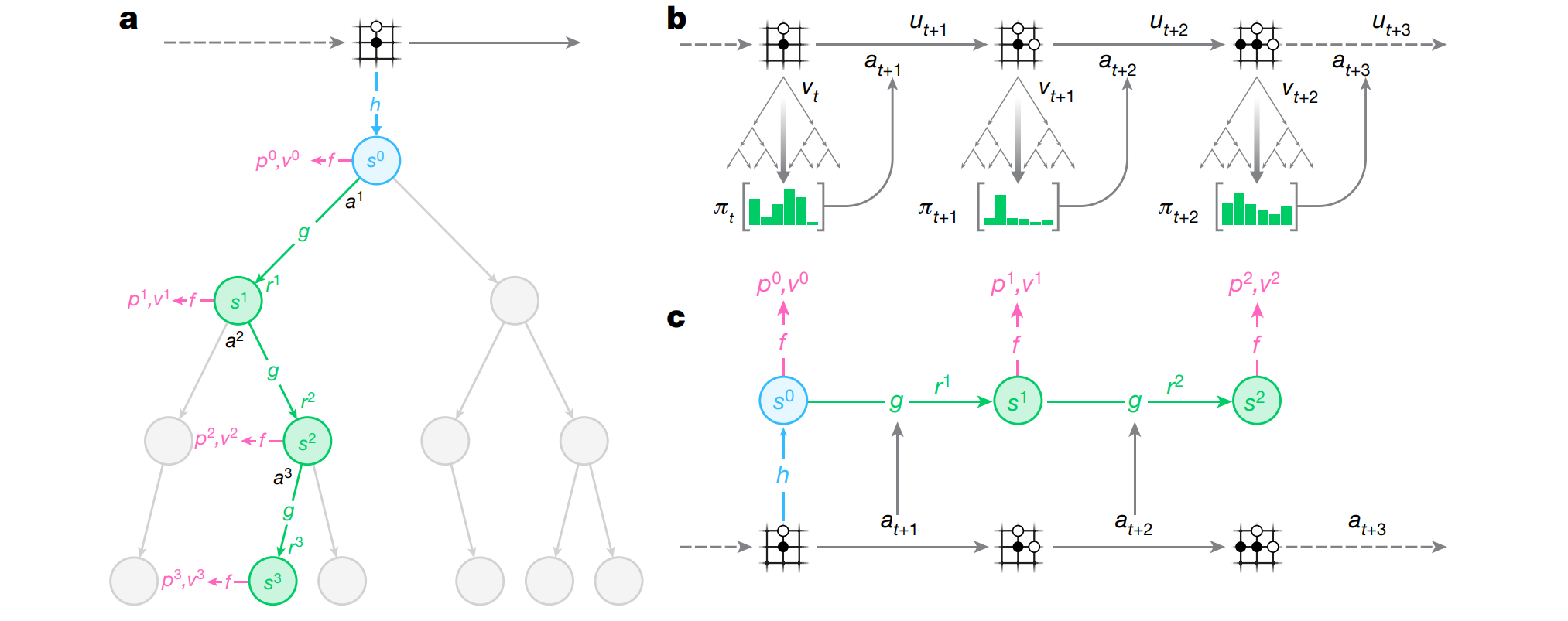
a) Search Phase

我们知道，之前版本的AI的MCTS是基于游戏引擎进行搜索。而MuZero是基于model的搜索，具体而言，我们有以下model：

h = f_\theta(s) \\\langle r, h' \rangle = g_\phi(h, a) \\\langle p, v \rangle = f_\xi(h)

其中， $f_\theta$ 作为encoder，将state $s$ encode成hidden vector $h$ ; $g_\phi$ 作为model dynamics，将state $s$ 的hidden vector $h$ 和action $a$ 作为输入，预测下一个state $s'$ 的hidden vector $h'$ 和reward signal $r$ ； $f_\xi$ 作为 policy 和 value head，将state $s$ 的hidden vector $h$ 作为输入，输出predicted winning rate $v$ 和 action probability $p$ 。这里隐含了一个假设，也就是 $h' \approx f_\theta(s')$ 。

我们简化下：

\langle p, v \rangle = f_\xi(f_\theta(s)) \\\langle r, h' \rangle = g_\phi(f_\theta(s))

相比于之前的版本，这里无非是用一个neural network来近似本来需要用游戏引擎得出的搜索结果。

b) Play Phase

这部分没什么好讲的，跟之前版本一样，只不过在储存数据时，储存的不是single transition，而是整个episode；这样在training phase中，sample的数据也是一整个episode。

c) Training Phase

在之前的版本中，training sample 都是single transition，而因为我们的model dynamics时recurrent function，所以我们sample 一个长度为 $K$ 的concurrent transtions，文中取 $K = 5$ 。损失函数如下:

L_t(\theta, \phi, \xi) = \sum_{k=0}^{K} l^p(\pi_{t+k}, p_t^k) + \sum_{k=0}^{K} l^v(z_{t+k}, v_t^k) + \sum_{k=0}^{K} l^r(u_{t+k}, r_t^k) + c (\|\theta\|^2 + \|\phi\|^2 + \|\xi\|^2)

第一项是policy cross enctropy loss，第二项是value loss，第三项是reward signal loss，最后一项是parameter regularization。

对于zero-sum two player board game，第一，二项与之前版本相同，第三项设intermediate reward为0，而final step reward为游戏胜负 $u_t \in \{-1, 0, 1\}$ 。

对于atari game则稍微复杂些， $u_t$ 为immediate reward， $z_t$ 为n-step return，此外还做了大量的rescaling的tricks，且用了DRL之中的categorical distribution之类的innovation。