Problem 1.
199200 和 200199哪个大?
Solution
对付这一类型的题目,手算对数最简单无脑。
ln(1+x)=x−21x2+31x3+… 那么
ln1−x1+x=2(x+31x3+51x5+…) 我们设
f(x)=2(x+31x3+51x5+…) 那么
ln256−ln200=ln1−56/4561+56/456=f(45656) ln256−ln199=f(45557) ==199ln200−200ln199200f(56/456)−199f(57/455)−ln256199(f(56/456)−f(57/455))+f(56/456)−ln256 显然
f(56/456)<f(57/455),f(56/256)<1<ln(256) 所以
199ln200−200ln199<0,200199<199200 具体来算
ln2=f(1/3)≈2(1/3+1/34+1/5×1/35)≈0.693ln200=8ln2−f(56/456)≈5.544−2×56/456=5.298ln199=8ln2−f(57/455)≈5.544−2×57/455=5.293199ln200≈1054.3200ln199≈1059.6 Problem 2.
圆上任选三点组成三角形,这个三角形是锐角、钝角和直角三角形的概率分别是多少?
Solution
任取三点,三角形为锐角,等价于
A:θ1∈[0,2π]B:θ2∈[θ1+π,θ1+2π]C:θ3∈[θ2−π,θ1+π] 根据贝叶斯
P(A,B,C)=P(C∣A,B)P(A,B)=P(C∣A,B)P(B∣A)P(A) 很显然
P(A)=1P(B∣A)=2ππ=0.5 设x=θ2−θ1, 那么
P(C∣A,B)=∫π2π2π1dx=0.5 所以
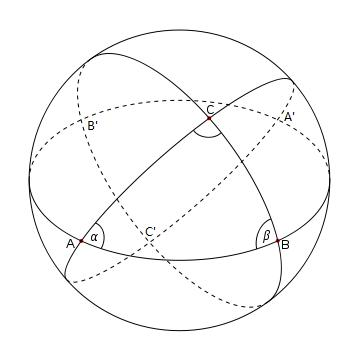
P(A,B,C)=0.25 四点包球的情况,其实也很简单。任取单位球面三点 A,B,C ,构成球面三角形。其球心对称点为 A′,B′,C′ ,那么如果点 D∈△A′B′C′ ,则四点包圆。以下所有三角形都是指球面三角形。
X:A,B,C∈⊙RY:D∈△A′B′C′ 那么
P(X,Y)=P(Y∣X)P(X) 显然,P(X)=1,且有
P(Y∣X)=∫△A′B′C′4πS(△A′B′C′)p(△A′B′C′)=∫△ABC4πS(△ABC)p(△ABC) S(△ABC)+S(△A′BC)=2πα×4π=2αp(△ABC)=p(△A′BC) 所以
2P(Y∣X)=∫0π4π2απ1dα=4π2α2∣0π=41 P(X,Y)=81 Problem 3.
已知a,b,c∈{R}+,a+b+c=1,证明a2+b2+c2+2abc∈[11/27,1)
Solution
问题等价于以下求 f(x,y) 的极值:
f(x,y)=x2+y2+(1−x−y)2+2xy(1−x−y)1>x>0,1>y>0,x+y<1 易知
f(x,y)=f(y,x)dxdf=2x+2(x+y−1)+2y−4xy−2y2=4x+4y−4xy−2y2−2dxdyd2f=4(1−x−y)>0dx2d2f=4(1−y)>0 所以曲面 z=f(x,y) 为凹面,且关于 x=y 对称。那么 z=f(x,y) 的极小值点必然在对称面与曲面的交线上,也就是 g(x)=f(x,x)=2x2+(2x−1)2+2x2(1−2x),0<x<1/2 这条线上。令g′(x)=0 则有
8x−6x2−2=0x=1,x=31 只有 x=1/3 在定义域,所以 g(x)≥g(1/3)=11/27 ,且 g(x)<max(g(0),g(1/2))=1。同时,很容易知道, f(x,y) 的最大值在边界上,也就是f(1/2,1/2),f(0,1),f(1,0),f(0,0) 其中一点上,而这些值中最大为1,所以
2711≤f(x,y)<1 Problem 4.
如何确定 Vasile 不等式 (a2+b2+c2)2≥3(a3b+b3c+c3a) 的取等条件?
Solution
其非平凡取等条件为
a:b:c=sin274π:sin272π:sin27π 借用python的sympy解一下高次方程,好像很容易的样子。
设f(a,b,c)=LHS−RHS≥0,则有
∂a∂f∂b∂f∂c∂f=2(a2+b2+c2)2a−3(3a2b+c3)=…=…=0=0=0 设a=k,b=xk,c=yk,k=0,则有
4(1+x2+y2)−3(3x+y3)=04(1+x2+y2)x−3(3x2y+1)=04(1+x2+y2)y−3(3y2+x3)=0 那么
3x2+y3x−3x2y−1=03xy+y4−3y2−x3=0 再设 x=rsinθ,y=rcosθ ,则有
r2cos4θ−rsin3θ+3sinθcosθ−3cos2θ=0 令cosθ>0,因为x=ytanθ,则有
y2cos2θ−xsin2θ+3cosθsinθ−3cos2θ=0y=rcosθ=(tan3θ+tan6θ−12tanθ+12)/2 所以
3y2tan2θ+y4tanθ−3y3tan2θ−1=0 我们设t=tanθ,用sympy解得
(t−1)(t3−5t2+6t−1)(t3+2t2−t−1)(t6+4t5−12t4−6t3+25t2−12t+1)=0 除去虚数根和平凡解t=1,只需验证满足
t=a/b,b/c,c/a 中任意一个即可。我们发现 t3−5t2+6t−1=0的三组解正好满足条件。接下来用三角函数法解此三次方程即可。我们考虑
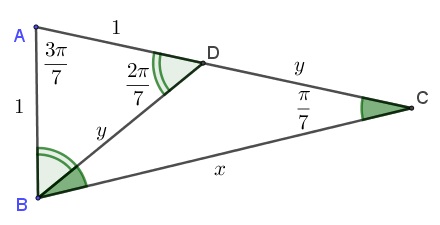
t=cb=4cos27π=2(1+cos72π) 考虑以下三角形
注意这里三角形的x,y与上面a,b,c转换用的x,y含义不同。易知x=y+1,且有
cos∠ADB=2y=2t−1 则有t=y+2=x+1,又有
cos∠C=2yx=2x22x2−1 那么
t−2t−1=(t−1)22(t−1)2−1 即
t3−5t2+6t−1=0