我们前面提到的蒙特卡洛树搜索，其实颇有强化学习的影子。而接下来我们会看到，learning和searching在解决问题上的共通和不同之处，以及他们融合之后的强大。

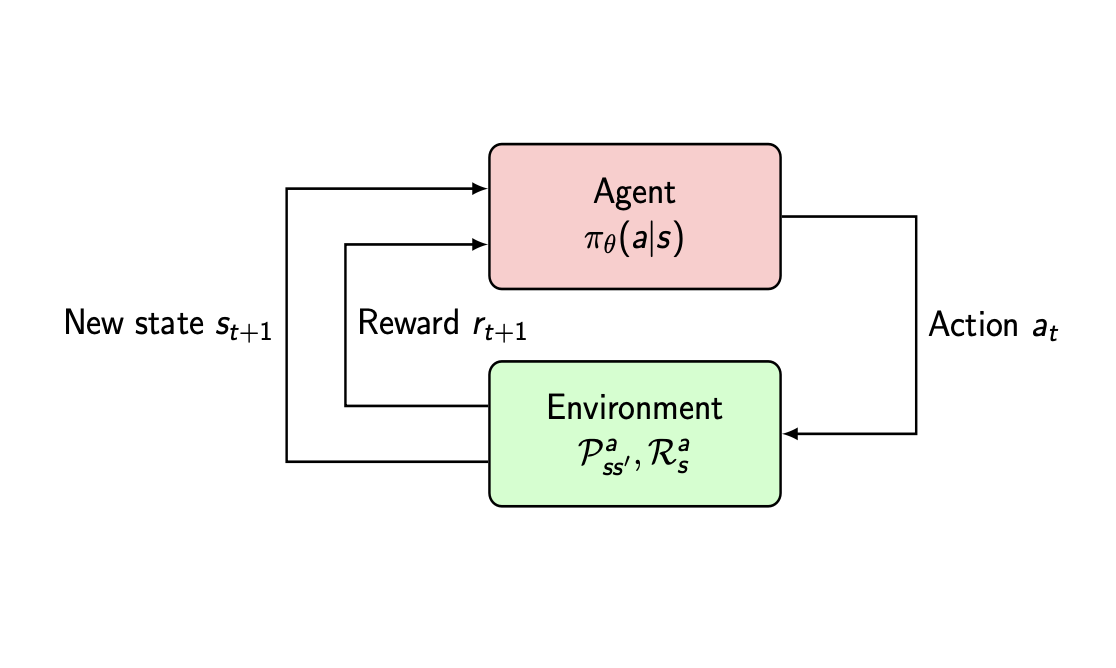
我们常说的强化学习包含两个要素：Agent和Environment。而学习的目标是指，Agent学到一个优秀的策略，使之与Environment互动中，获取更多的Reward；这个过程，就很像生物与环境的互动了。

Reinforcement Learning and Optimal Control

强化学习的数学模型脱胎于最优控制Optimal Control，我们甚至会发现，他们不过是同一问题的不同表述，以至于他们的数学形式都非常相似:

Reinforcement Learning:
$\begin{aligned} \text{maximize } \quad & \mathbb{E}_{\tau\sim\pi} \{ \sum_{t=0}^N \gamma^t r_{t+1} \}\\ \text{subject to} \quad & r_{t+1} \sim \mathcal{R}(s_t, a_t) \\ & a_t \sim \pi(a|s_t)\\& s_{t+1} \sim \mathcal{P}(s_{t}, a_t)\\& \tau = s_0, a_0, r_1, s_1, a_1, r_2 \dots \end{aligned}$
Optimal Control:
$\begin{aligned} \text{minimize } \quad & \mathbb{E}_{\tau \sim \pi}\{\sum_{k=0}^N g_k(x_k, u_k) \} \\ \text{subject to} \quad & x_{k+1} = f_k(x_k, u_k) \\ & u_k = \pi_k(x_k) \\ & \tau = x_0, u_0, x_1, u_1, \dots \end{aligned}$

在optimal control的框架内，system dynamics和control policy往往被近似为linear或者quadratic的form，如此，在某个time-step下，该问题就是简单的convex optimisation的问题；再套用dynamic programming，从 $k=N$ 求解到 $k=0$ ，即可求得所有的control signal $u_0, u_1, \dots, u_{N-1}$ ，亦即control policy $\pi$ 。

而在reinforcement learning的框架内，system dynamics和control policy更多是non-deterministic且non-linear的，亦或是未知的，套用optimal control的方法往往会面临诸多困难。所以，RL发展出了另一套基于Markov Decision Process的数学框架。

Markov Decision Process

作为RL的理论基础:

A Markov Decision Process is a 4 tuple $(\mathcal{S, A, R,P})$ where:
$\mathcal{S}$ is the set of state space
$\mathcal{A}$ is the set of action space
$\mathcal{R}$ is reward function: $\mathcal{R:S \times A} \rightarrow \mathbb{R}$
$\mathcal{P}$ is transition probability: $\mathcal{P:S\times A \times S}\rightarrow [0, 1]$

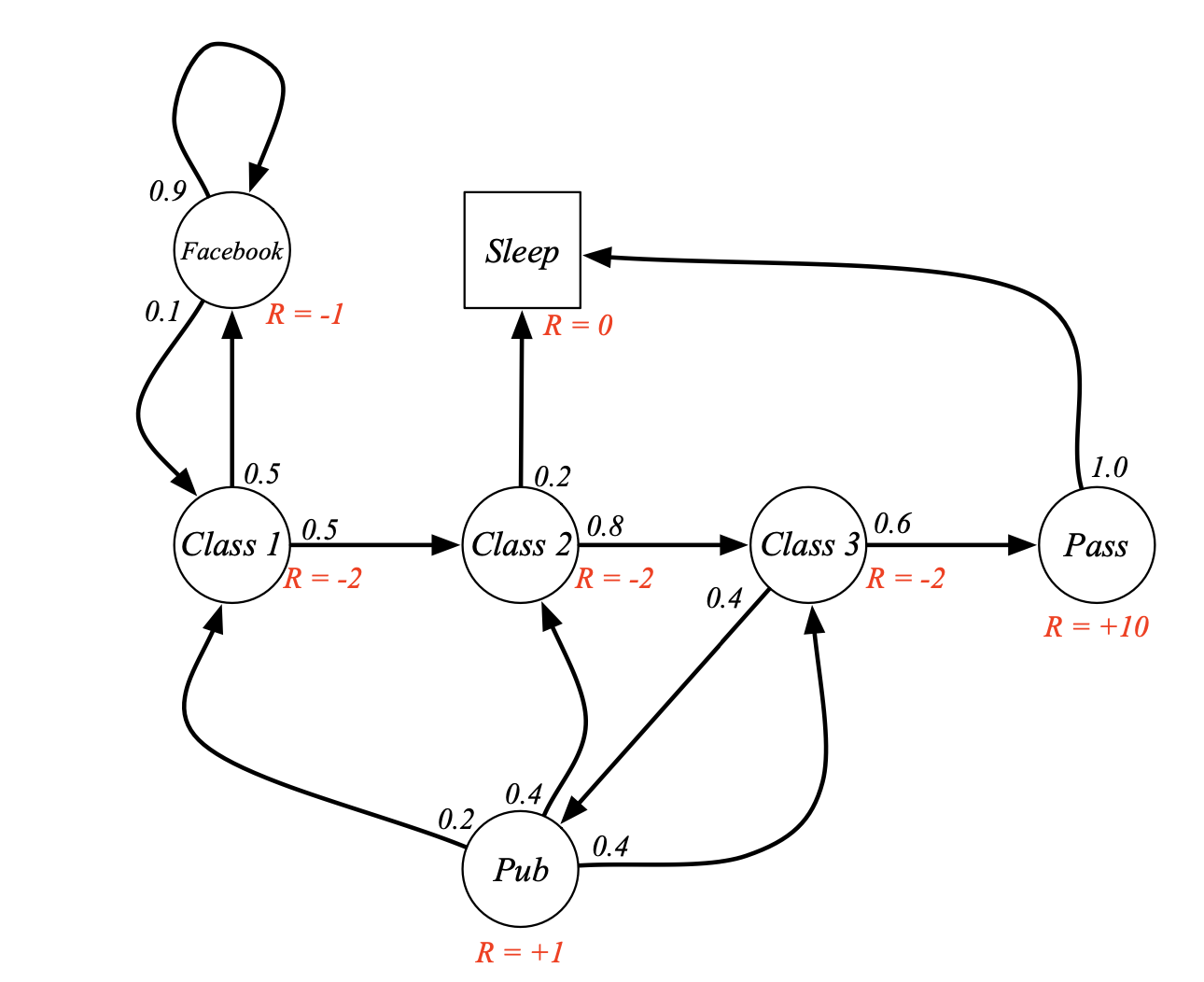
下图摘采自David Silver的lecture notes，图节点代表states，箭头代表state transition probability，相比于图中MDP，RL在应用层面的MDP往往要复杂的多：

State/Action space is high dimensional/continous/finite
Reward function is non-deterministic

在做RL理论研究时，为了简化问题，往往会将state space和action space设计为finite and discrete，reward function为deterministic，这种设计称之为tabular solution。对于上图所示给定策略的MDP， $\mathcal{P}$ 为 $|\mathcal{S}| \times |\mathcal{S}|$ 的probabililty tensor， $\mathcal{R}$ 为 $|\mathcal{S}|$ 的向量：

\mathcal{P} = \begin{matrix}C1 & C2 & C3 & Pass & Pub & FB & Sleep \\\hline0 & 0.5 & 0 & 0 & 0 & 0.5 & 0 \\0 & 0 & 0.8 & 0 & 0 & 0 & 0.2 \\0 & 0 & 0 & 0.6 & 0.4 & 0 & 0 \\0 & 0 & 0 & 0 & 0 & 0 & 1 \\0.2 & 0.4 & 0.4 & 0 & 0 & 0 & 0 \\0.1 & 0 & 0 & 0 & 0 & 0.9 & 0 \\0 & 0 & 0 & 0 & 0 & 0 & 1 \\\end{matrix}

\mathcal{R} = \begin{matrix}C1 & C2 & C3 & Pass & Pub & FB & Sleep \\\hline-2 & -2 & -2 & 10 & 1 & -1 & 0 \\\end{matrix}

如何评价某个状态的好坏？我们以Pub为例，从此状态开始采样轨迹:

\begin{aligned}\tau_1 &= Pub, C1, C2, C3, Pass, Sleep\\\tau_2 &= Pub, C2, Sleep \\\tau_3 &= Pub, C3, Pub, C1, FB, C1, C2, Sleep\\&\dots\end{aligned}

计某个轨迹的累积奖励为 $G$ ，那么

\begin{aligned}G(\tau_1) &= +1-2-2-2+10+0\\G(\tau_2) &= +1-2+0 \\G(\tau_3) &= +1-2+1-2-1-2-2+0\\& \dots\end{aligned}

那么Pub的平均累计奖励

V(s_\text{pub}) = \frac{G(\tau_1) + G(\tau_2) + G(\tau_3) + \dots + G(\tau_N)}{N}

即可作为评估其好坏的指标。若是已知 $V(s_\text{C1}), V(s_\text{C2}), V(s_\text{C3})$ ，又有:

V(s_\text{pub}) = 1 + 0.2\times V(s_\text{C1}) + 0.4\times V(s_\text{C2})+0.4\times V(s_\text{C3})

对于以上MDP，已知 $\mathcal{P,R}$ ，对于求出 $V$ 显然是完备的，具体来说：

V = \mathcal{R + P}V \\ V = (I - \mathcal{P})^{-1}\mathcal{R}^T

Reinforcement Learning

对于RL，我们再定义

RL Basis
Policy function $\pi: \mathcal{S \times A} \rightarrow [0, 1]$
Value function $V: \mathcal{S} \rightarrow \mathbb{R}$
Discount factor $\gamma \in (0, 1]$
Episodic trajectory $\tau = (s_0, a_0, r_1, s_1, a_1, r_2, \dots)$ where $s_0 \sim d_0(s), a_0 \sim \pi(s_0), r_1 \sim \mathcal{R}(s_0, a_0), s_1 \sim \mathcal{P}(s_0, a_0), \dots$
Discounted return $G(\tau) = r_1 + \gamma r_2 + \gamma^2 r_3 + \dots = \sum_{t=0}^T\gamma^t r_{t+1}$

我们注意到，如果 $\gamma \in (0, 1)$ 的话， $G(\tau) \leq r_{\max}/(1 - \gamma)$ ，可见，discounted factor作用是使得discounted return bounded。

RL的优化目标为寻找最优策略：

\pi^* = \max_\pi \mathbb{E}_{\tau \sim \pi }[G(\tau)]

为此，大致衍生出两种解法，一种是直接take gradient的policy gradient，一种是基于值函数的TD learning；而两者之混合产生了更为优秀的解法，称之为actor critic。

Policy Gradient Method

PG的数学稍微有点意思:

我们定义某个策略 $\pi$ 的expected total discounted return

\begin{aligned}\eta(\pi) &= \mathbb{E}_{\tau \sim \pi}[G(\tau)] \\&= \int_{\tau \in \mathcal{T}(\pi)} p(\tau)G(\tau) d\tau\end{aligned}

其中 $\mathcal{T}(\pi)$ 为所有轨迹的集合。对于某个采样到的episodic trajectory $\tau = (s_0, a_0, r_1, s_1, a_1, r_2, \dots)$

p(\tau) = d(s_0) \prod_{t=0}^T \pi(s_t, a_t)\mathcal{P}(s_t, a_t, s_{t+1}) \\G(\tau) = \sum_{t=0}^T \gamma^t r_{t+1}

对于带有参数的策略 $\pi_\theta$ ，我们求其梯度

\begin{aligned} \nabla_\theta \eta(\pi_\theta) &= \int \nabla_\theta p_\theta(\tau) G(\tau) d\tau \\ &= \int p_\theta(\tau)\nabla_\theta \log p_\theta(\tau)G(\tau)d\tau \\ &= \int p_\theta(\tau) \nabla_\theta[\log d(s_0) + \sum_{t=0}^T \log\pi_\theta(s_t, a_t) + \sum_{t=0}^T\log\mathcal{P}(s_t, a_t, s_{t+1})]G(\tau)d\tau \\ &= \int p_\theta(\tau)\sum_{t=0}^T\nabla_\theta \log\pi_\theta(s_t, a_t)G(\tau) d\tau \\ &= \mathbb{E}_{\tau \sim p_\theta(\tau)}[(\sum_{t=0}^T\nabla_\theta \log \pi_\theta(s_t,a_t))(\sum_{t=0}^T\gamma^tr_{t+1})] \end{aligned}

依此，即可得到经典的REINFORCE算法:

REINFORCE Algorithm
Sample episodic trajectory $\{\tau_i\}$ from $\pi_\theta(s, a)$
Calculate $\nabla_\theta \eta(\pi_\theta) \approx \sum_i(\sum_t \nabla_\theta \log \pi_\theta(s_{i,t}, a_{i,t}))(\sum_t \gamma^tr_{i, t+1}))$
Update policy $\theta \leftarrow \theta + \alpha \nabla_\theta \eta(\pi_\theta)$

Value Function Method

我们定义值函数

V_\pi(s) = \mathbb{E}_{\tau \sim \pi, s_0 = s}[G(\tau)]

即：以 $s$ 为起始状态， $\pi$ 为采样策略的episodic trajectory的discounted return的期望值。由此

\begin{aligned}V_\pi(s) &= \mathbb{E}_{a\sim\pi}[\mathcal{R}(s,a) + \gamma G_{t+1}|S_t=s] \\&= \sum_{a\in \mathcal{A}}\pi(s,a)\sum_{s'\in \mathcal{S}}p(s'|s,a)[r(s,a) + \gamma V_\pi(s')] \\&= \sum_{a\in\mathcal{A}}\pi(s,a)r(s,a) + \gamma\sum_{a\in\mathcal{A}}\sum_{s'\in\mathcal{S}}p(s'|s,a)\pi(s,a)V_\pi(s')\end{aligned}

我们定义Q函数

Q_\pi(s,a) = \mathbb{E}_{\tau\sim\pi, s_0=s, a_0=a}[G(\tau)]

即：以 $s$ 为起始状态， $a$ 为起始动作， $\pi$ 为采样策略的episodic trajectory的discounted return的期望值。由此

\begin{aligned}Q_\pi(s,a) &= r(s,a) + \gamma\sum_{s'\in\mathcal{S}}p(s'|s,a)V_\pi(s')\end{aligned}

我们很容易得出

V_\pi(s) = \sum_{a\in\mathcal{A}}\pi(s,a)Q_\pi(s,a)

Q_\pi(s,a) = r(s,a) + \gamma\sum_{s'\in\mathcal{S}}p(s'|s,a)\sum_{a'\in\mathcal{A}}\pi(s',a')Q_\pi(s',a')

我们称上面两个公式为Bellman Equations for on-policy value function。

对于最优策略 $\pi^*$ , 其对应的optimal solution

\begin{aligned}V^*(s) &= \max_{a} Q^*(s,a) \\&= \max_a \sum_{s'\in \mathcal{S}}p(s'|s,a)[r(s,a) + \gamma V^*(s')] \\\end{aligned}

\begin{aligned}Q^*(s,a) &= r(s,a) + \gamma\sum_{s'\in\mathcal{S}}p(s'|s,a)V^*(s') \\&= r(s,a) + \gamma\sum_{s'\in\mathcal{S}}p(s'|s,a)\max_{a'}Q^*(s',a')\end{aligned}

我们称上面两个公式为Bellman Optimal Equations 。

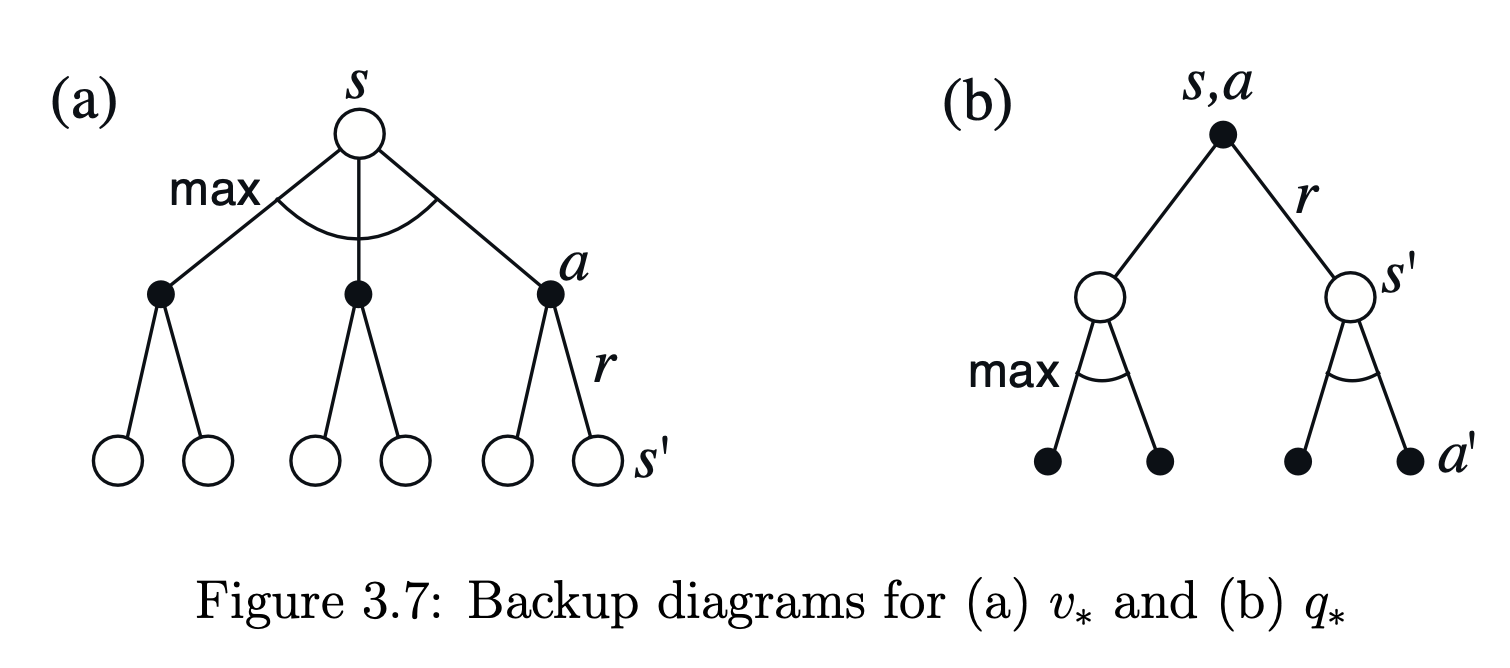
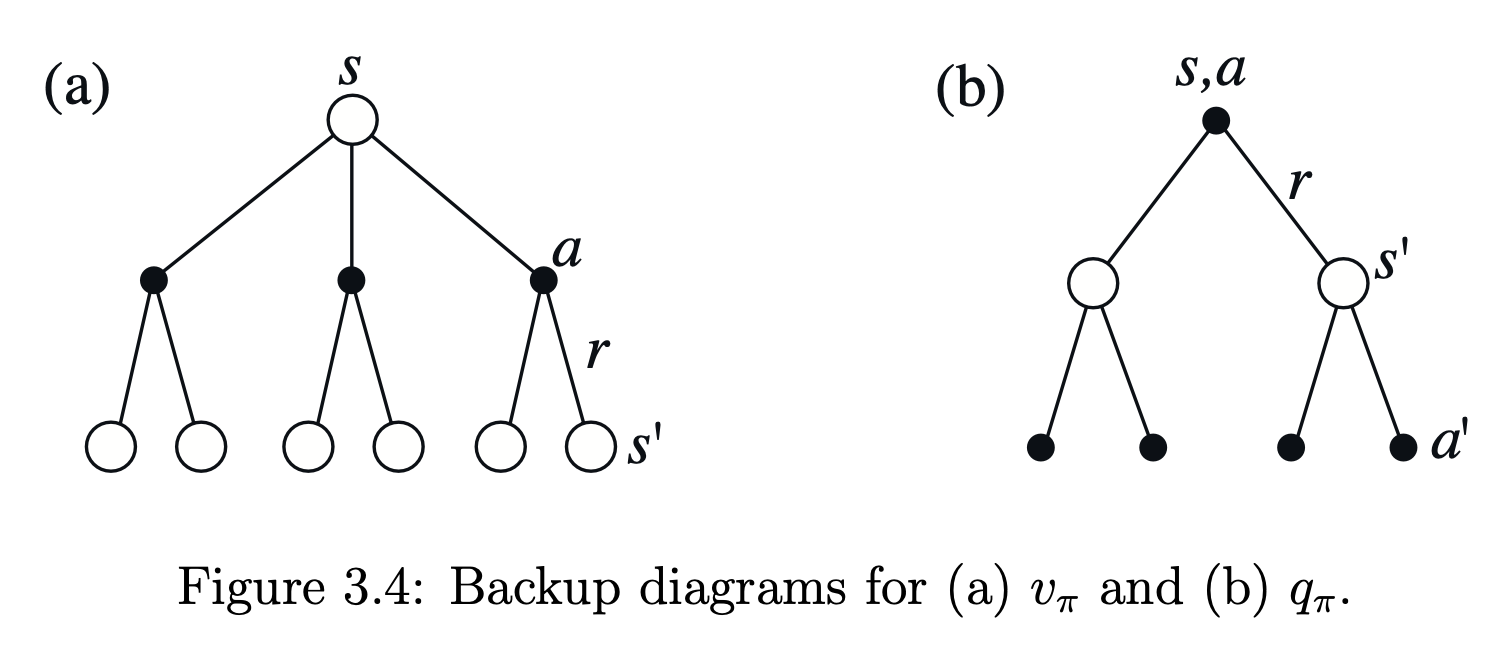
借用Sutton的的书中第三章的图，以描述Q函数和值函数及其opitmal solution

看到这两张图，应该会想起MCTS的吧～

下面我们给出Value Iteration算法:

Value Iteration:
Randomly initialise $V(s)$
$\Delta \leftarrow 0$ , for each $s \in \mathcal{S}:$
$\begin{aligned} & v \leftarrow V(s) \\ & V(s) \leftarrow \max_a \sum_{s'\in \mathcal{S}}p(s'|s,a)[r(s,a) + \gamma V^*(s')] \\ & \Delta = \max(\Delta, |v- V(s)|)> \end{aligned}$
Repeat step 2 until $\Delta$ is sufficient small
Output policy $\pi(s) = \arg\max_a \sum_{s'\in \mathcal{S}}p(s'|s,a)[r(s,a) + \gamma V^*(s')]$

我们注意到，VI算法的缺点在于需要知道model的transition probability $p(s'|s,a)$ ；而现实中，很多问题的model并不available，这种情况下，我们只好进行估算，比如Monte Carlo Control：

Monte Carlo Control:
Randomly initialize $\pi(s), Q(s,a)$ , create a list dictionary $R(s,a)$
Loop for each episode:
Generate trajectory $s_0, a_0, r_1, s_1, a_1, \dots, s_T$ with $a \sim \pi(s)$ , $G \leftarrow 0$
For timestep $t = T-1, T-2, \dots, 0$ :
$G \leftarrow \gamma G + r_{t+1}$
Append $G$ to $R(s_t,a_t)$
$Q(s_t,a_t) = \sum R(s_t,a_t) / |R(s_t, a_t)|$
$\pi(s_t) = \arg\max_a Q(s_t, a)$

我们看到Monte Carlo Control 本质上是在通过采样的方法估算Q函数:

\begin{aligned}Q^*(s,a) &= \mathbb{E}_{\tau \sim \pi^*, s_0=s, a_0=a} [G(\tau)] \\&\approx \frac{1}{N}(G(\tau_1) + G(\tau_2) + \dots +G(\tau_N)) \\\end{aligned} \\ \text{where} \quad \tau_n \sim \pi^* \quad \text{with} \quad s_0=s, a_0=a

更进一步，我们可以

\begin{aligned}Q^*(s,a) &= r(s,a) + \gamma \mathbb{E}_{s'}[\max_{a'} Q(s',a')] \\&\approx r(s,a) + \gamma \frac{1}{N}(\max_{a'}Q(s'_{1},a') + \max_{a'}Q(s'_{2},a') + \dots + \max_{a'}Q(s'_{N}, a'))\end{aligned}

依此，给出Q Learning 算法

Q Learning:
Randomly initialise $Q(s,a)$ , $\epsilon$ -greedy policy $\pi_Q$ , learning rate $\alpha$
Loop for each episode:
For each time-step $t$ :
$_t \sim \pi_Q(s)$
$Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha[r_{t+1} + \gamma \max_aQ(s_{t+1}, a) - Q(s_t, a_t)]$

所谓的 $\epsilon$ -greedy policy:

\pi(s)= \begin{cases}a \sim \mathcal{A}/a^*, x \geq \epsilon \\a^*, x < \epsilon\end{cases}\\\text{where} \quad a^* = \arg\max_aQ(s,a), x \sim [0, 1]\\

在estimate $\max_{a'}Q(s',a')$ 的时候，我们用exponential running average代替了原本的mean，因为我们认为，随着learning的继续，我们的optimal Q estimation会越来越接近真实值。

Actor Critic Method

我们之前提到的REINFORCE算法在实际应用中，会存在很大问题：

样本利用率过低。采样N个trajectory，policy才更新一次；相对于单个元组 $<s, a, r>$ 即可更新的Q learning，对数据的利用率太低。
梯度噪音过大。如果environment够丰富的话，相对于整个轨迹空间，采样到的轨迹的分布的覆盖率可能微乎其微，甚至过于集中，这样得到的梯度偏差非常大，以至于下次采样得到的轨迹分布更加不均匀，陷入恶性循环，导致学习失败。
Return的分布问题。如果environment的reward全是非负，或者非正，那么gradient的方向便是一边倒，如果policy用的是neural network，则很容易出现数值溢出的问题，导致学习失败。

对于问题3，我们取一个baseline，

b = \frac{1}{N}\sum_{i=1}^N G(\tau_i)

让每一个trajectory的return减去这个baseline以区分不同trajectory的偏向，我们发现policy gradient

\begin{aligned}\nabla_\theta \eta(\pi_\theta) &= \int \nabla_\theta p_\theta(\tau) (G(\tau)-b) d\tau \\&= \int \nabla_\theta p_\theta(\tau) G(\tau) d\tau - \int \nabla_\theta p_\theta(\tau) b d\tau \\&= \int \nabla_\theta p_\theta(\tau) G(\tau) d\tau - b \nabla_\theta\int p_\theta(\tau) d\tau \\&= \int \nabla_\theta p_\theta(\tau) G(\tau) d\tau - b \nabla_\theta 1 \\&= \int \nabla_\theta p_\theta(\tau) G(\tau) d\tau\end{aligned}

并没有被影响到。

对于问题1，我们很容易想到用experience replay的办法来解决，即：我们将采集到的 $<s,a,r>$ 元组放在一个fixed size pool中，每次更新，从里面随机抽取一部分元组求梯度即可。接下来，我们考虑单个元组对policy gradient的贡献：

\mathbb{E}_{\tau\sim p_{\theta'}(\tau)} [\nabla_\theta \log\pi_\theta(s_t, a_t)G(\tau)] \\

这里又涉及到两个问题：

Causality的问题。从因果关系上讲， $\pi(s_t,a_t)$ 影响不了已经发生的 $\sum_{t'=0}^t \gamma^{t'}r_{t'+1}$ 。从梯度区分度上讲，在同一个trajectory中，不同的元组，对梯度的偏向权重相同，都是 $G(\tau)=\sum_t \gamma^tr_{t+1}$ 。
Off-policy的问题。我们注意到，使用experience replay，会导致更新policy用的经验，可能并不是当前待更新的policy产生的，这与我们推导出的policy gradient的要求不符。

对于causality的问题，我们考虑用 $Q(s_t, a_t)$ 来代替 $G(\tau)$ 来解决。这种情况下，我们用 $V(s_t)$ 做为baseline以区分gradient偏向，我们定义advantage function $A(s_t, a_t) = Q(s_t, a_t) - V(s_t) = r_t + \gamma V(s_{t+1}) - V(s_t)$ ，那么单个元组对policy gradient的贡献为

\nabla_\theta \eta(\pi_\theta) = \mathbb{E}_{\tau\sim p_{\theta'}(\tau)} [\nabla_\theta \log\pi_\theta(s_t, a_t)A(s_t, a_t)] \\

对于off-policy的问题，考虑importance sampling

\begin{aligned}\mathbb{E}_{x\sim p(x)}[f(x)] &= \int p(x)f(x)dx \\&= \int \frac{q(x)}{p(x)}p(x)f(x)dx \\&= \int q(x)\frac{p(x)}{q(x)}f(x)dx \\&= \mathbb{E}_{x\sim q(x)}[\frac{p(x)}{q(x)}f(x)]\end{aligned}

Importance Sampling的意义是，如果我们的数据 $x$ 是从 $q(x)$ 分布采样获得，而我们要计算 $f(x)$ 在 $p(x)$ 分布下的期望，应该如何转换。那么对于off-policy，

\begin{aligned}\nabla_\theta \eta(\pi_\theta) &= \nabla_\theta \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[G(\tau)] \\&= \nabla_\theta \mathbb{E}_{\tau \sim p_{\theta'}(\tau)}[\frac{p_\theta(\tau)}{p_{\theta'}(\tau)}G(\tau)]\end{aligned}

注意到

\begin{aligned}\frac{p_\theta(\tau)}{p_{\theta'}(\tau)} &= \frac{p(s_0)\prod_t\pi_\theta(s_t,a_t)p(s_{t+1}|s_t,a_t)}{p(s_0)\prod_t\pi_{\theta'}(s_t,a_t)p(s_{t+1}|s_t,a_t)} \\&= \frac{\prod_t\pi_\theta(s_t,a_t)}{\prod_t\pi_{\theta'}(s_t,a_t)}\end{aligned}

如此，我们得到修正后的policy gradient

\begin{aligned}\nabla_\theta\eta(\pi_\theta) &= \mathbb{E}_{\tau\sim p_{\theta'}(\tau)} [\frac{\pi_\theta(s_t, a_t)}{\pi_{\theta'}(s_t,a_t)}\nabla_\theta \log\pi_\theta(s_t, a_t)A(s_t, a_t)] \\&\approx \frac{1}{N}\sum_{i=1}^N\ \frac{\pi_\theta(s_{t,i}, a_{t,i})}{\pi_{\theta'}(s_{t,i},a_{t,i})}\nabla_\theta \log\pi_\theta(s_{t,i}, a_{t,i})A(s_{t,i}, a_{t,i})\end{aligned}

以上即是Actor Critic的理论基础；据此，我们写出Offline Actor Critic算法：

Offline Actor Critic:
Randomly initialise policy network $\pi_\theta$ and value network $V_\phi$ , an empty replay buffer $\mathcal{R}$
Loop for each trajectory:
Loop for each time-step $t$ :
Sample $<s_t, a_t, r_t>$ from $\pi_\theta$ , record $\hat{\pi}_t = \pi_\theta(s_t,a_t)$
Periodically update, if $t \bmod T = 0$ , sample a batch of $N$ tuples $\{s_i, a_i, \hat{\pi}_i, r_i, s_i', g_i\}$ , calculate:
Advantage Function $A(s_i, a_i)=r_i + \gamma V_\phi(s_i') - V_\phi(s_i)$
Policy Gradient $\nabla_\theta \eta(\pi_\theta) = N^{-1}\sum_i \pi(s_i, a_i)\nabla_\theta \log \pi_\theta(s_i, a_i)A(s_i,a_i)/\hat{\pi}_i$
Value Gradient $\Delta\phi = N^{-1}\sum_i \nabla_\phi (V_\phi(s_i) - g_i)^2$
Update policy network: $\theta \leftarrow \theta + \alpha\nabla_\theta\eta(\pi_\theta)$
Update value network: $\phi \leftarrow \phi - \beta \Delta\phi$
Calculate discounted sum rewards: $g_t= r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + \dots$
for each timestep, and push $<s_t, a_t, \hat{\pi}_t, r_t, s_{t+1}, g_t>$ into replay buffer $\mathcal{R}$

SuttonBartoIPRLBook2ndEd.pdf