关于深度学习，网上的教程很多，很多也写的比我好，这里仅从自己的角度，简单谈谈对深度学习的理解。

历史 History

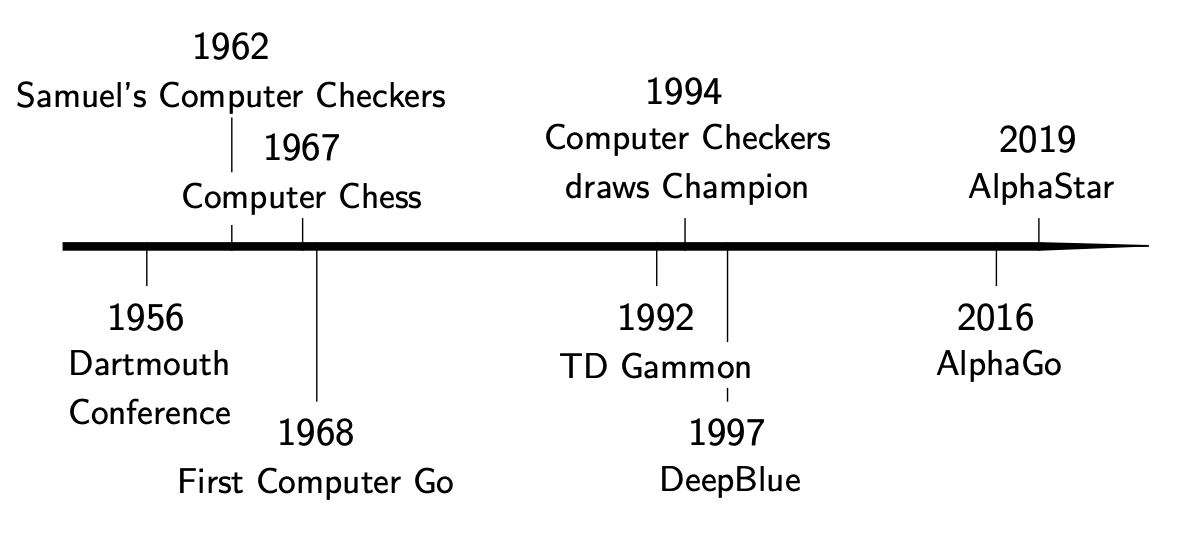
人工智能的历史，可能和数字计算机的历史一样长。早期人们设计AI程序，更多的是为了测试和展示计算机和算法，吸引公众注意；在应用领域，其实一直很狭窄，比如1950年香农设计的机械鼠Theusus，能够解决简单的迷宫问题。1956年的达特矛斯会议，堪比AI届的索尔维会议，现代AI的很多概念和框架，在那场会议中都有提及和确立。这之后，随着计算机算力的提升和算法的进步，AI在各种智力游戏竞赛中逐个击败人类；而这些历史事件，往往会引爆公众的讨论和焦虑，也伴随着资本的潮起潮落。

如果你将这些历史事件放在时间轴上看的话，很容易发现AI的三次浪潮所对应的时间分段；这其中，以本次AI浪潮最为汹涌，对人类社会的影响，我认为也最为深远。

人工智能下的各种理论，流派，分支，非常繁多；再加上媒体的渲染，很多时候连从业者都很难说清楚其中的边界；仅讨论当下最常见的三个术语之间的关系，可能会是这样：

基础 Foundations

要理解深度学习的基础，拿这分类，回归和拟合三个问题来做讨论恐怕最合适不过了，因为深度学习的诸多课题，其实都能在这三个问题中找到雏形。

分类 Classification

Given data points  $X =\{x_i |i = 1,2, \dots, K; x_i \in \mathbb{R}^N \}$  and $Y=\{y_i| i = 1, 2, \dots, M; y_i \in \mathbb{R}^N\}$, find $f_w$ such that

$$f_w(x) > 0, \forall x \in X \\ f_w(y) < 0, \forall y \in Y$$

从几何角度理解：

寻找一个$N$维曲面，使得所有$X$的点在曲面的一侧，所有的$Y$点在曲面的另一侧。

假设$f_w$为的second order polynomial function的话：

将$X,Y$代入，那么

$P = M + K$个不等式，$Q = 1+N+N^2$ 个变量。可简化为：

这就是一个简单的凸优化问题了。当$P > Q$时，可能出现无解的情况，增加$f_w$的polynomial degree即可。

回归 Regression

Given $X =\{x_i |i = 1,2, \dots, K; x_i \in \mathbb{R}^N \}$, find $f_w$ that minimise $\|f_w(X)\|$.

从几何角度理解：

寻找一个$N$维曲面，使得$X$中的点到曲面的距离之和最少。

我们同样假设$f_w$为second order polynomial function，同上，代入$X$，也可将问题转化为凸优化问题:

拟合 Curve Fitting

我们发现，无论是分类，还是回归，其实都是在做拟合: 分类问题其实在拟合数据边界，回归问题其实在拟合数据分布。很多情况下，也可以将其转化为简单的凸优化问题。但是，我们之前的模型很显然存在一个很大的问题：当数据在空间中的分布不符合我们的预期，即

1. 对分类问题，$\{w|Aw > 0\} = \empty$
2. 对回归问题，$\||f_w(X)\|$ 过大

我们当然可以通过增加$f_w$的order来解决，但随之而来的问题是$w$的维度$Q = 1 + N + N^2 + \dots$将成指数级增长，特别是当$N$本身很大时，这种解法简直是灾难。所以问题的关键在于$f_w$是polynomial这一假设，在某些数据分布下不适用，而强行增加polynomial的degree，会使得解出来的curve非常夸张。关于这一问题，PRML这本书的序章给出了很好的curve fitting的示例，我截图如下:

我们看到，当polynomial的order $M$过低时，拟合的曲线(红色)很难符合数据的真实分布(蓝点)，这个叫欠拟合(Under-fitting)。而当$M$过高时，虽然拟合的曲线穿过了所有的数据点($\|f_w(X)\|=0$)，但它造型夸张，与真实的数据分布想去甚远，这个叫过拟合(Overfitting)。

多层感知机 Multi Layer Perceptron

感知机 Perceptron

我们在上一节假设$f_w$是一个second order polynomial function，而感知机的模型更为简单，直接假设$f_w$是一个linear function:

很显然，这样的$f_w$对应的几何体，是一个超平面(hyperplane)，而这样的简单模型，也只能解决有限的问题。

激活函数 Activation Function

如果简单的进行函数嵌套，比如

那么

显然，嵌套后的复合函数依旧是个超平面，并没有什么效果。但是，如果给每个函数增加非线性性，那么结果就不一样了。比如

这里我们选择的这个非线性函数$\sigma(x)$就是非常著名的$ReLU$。而此时，这个增加了非线性激活函数的嵌套函数，就构成了所谓的多层感知机。我们上面的三层嵌套，也被称为三个隐藏层(hidden layer)。常见的激活函数可以参见Activation Function。

名由何来 Biological Inspiration

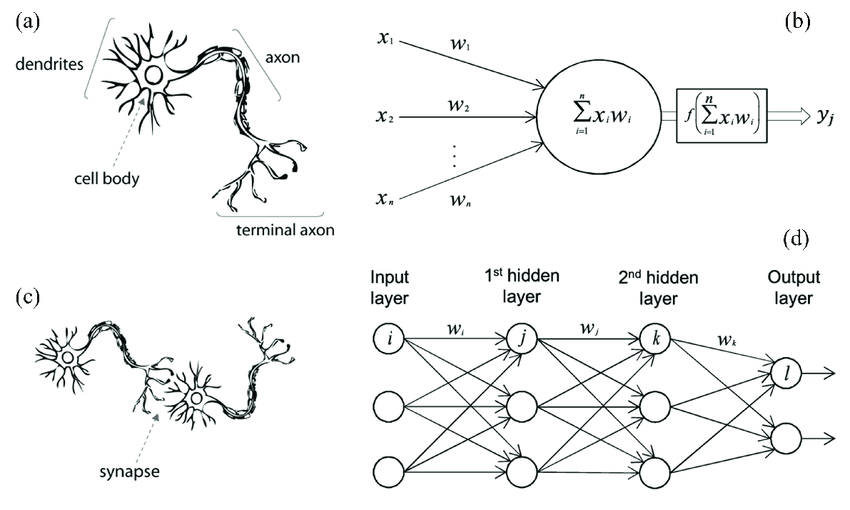
如果了解生物神经元的工作原理，就会发现其与我们上面介绍的感知机非常相似。生物神经元接受来自上一层神经元的刺激，在达到阈值时放电，将电信号通过轴突传导至下一层神经元，这其实就是$f_w(x) = \sigma(Ax+b)$，$x$ 是来自上层神经元的刺激，$A$是连接的权重，$b$是基底阈值，$\sigma$是激活模式。所以$f_w(z)$与单个视觉神经元的运作模式非常相似，而多层嵌套的非线性复合函数$f_W(z)$则与分层的生物视觉神经网络非常相似，多层感知机(MLP)便由此得名。

然而，即便是单个神经元，人工神经元的构造相比于生物神经元也显得太过粗糙，更何况生物神经元的种类和功能繁多，且神经元之间的通信机制不限于互相之间的神经连接。而生物神经网络，更是远比人工神经网络复杂和多变。先别说哺乳动物了，远比它低级的C. Elegans，其300余个神经元的位置，功能，连接已全部搞清楚，而且已经能在计算机上进行完整的模拟，然而其整个神经网络的协作和宏观表现，以及与其他生物信号之间的通信，我们还不能说完全弄清；所以，如今的人工神经网络框架，依然有非常大的进步空间。

梯度下降与反向传播 Gradient Descent and Back-propagation

这一步其实非常简单，只需要初步的高数知识。我们以regression为例:

Given $X \in \mathbb{R}^{M\times N}$ and $Y \in \mathbb{R}^N$, find $f_W$ that minimise $\|Y - f_W(X)\|$.

我们以L2 norm为例，

设损失函数，

我们对$L_W$一阶泰勒展开

当$\delta W = - L'(W)^T, \alpha \to 0^+$时，

也就是说，当$W$沿着$L'(W)$反方向小步移动后，$L(W)$的值会减少。这就是梯度下降法。

完整的算法：

1. Random initialisation $W \gets W_0$， a small learning rate $\alpha$
2. Calculate $\delta W = L'(W_{n-1}), W \gets W_{n} = W_{n-1} - \alpha \delta W$
3. If $|L(W_{n}) - L(W_{n-1})|$ is sufficient small, return $W_n$, else goto step 2

所以问题的关键是求$L'(W)$，用链式法则就好，我们设

那么

$L$对$b_1, b_2, b_3$的导数也可以此类推，非常简单，这就是所谓的反向传播。注意上式中 $\cdot$ 代表elementwise product，$\times$代表matrix multiplication，为了简洁，我们省略了括号，正确的操作顺序应该是从左到右(left to right)依次进行。根据以上，我们撸出MLP的代码，大家有兴趣可以更改下参数玩玩看:

import numpy as np
import matplotlib.pyplot as plt
fn = {
    'relu': lambda x: np.where(x < 0, 0, x),
    'l2': lambda x, y: 0.5 * (x - y) ** 2,
    'none': lambda x: x,
    'ce': lambda x: x
}

df = {
    'relu': lambda x: np.where(x < 0, 0, 1),
    'none': lambda x: 1,
    'l2': lambda x, y: x - y,
    'ce': lambda x: x
}

class LinearLayer:
    def __init__(self, in_dim, out_dim, act_fn, lr=0.1):
        self.W = np.random.randn(in_dim, out_dim) / in_dim
        self.b = np.random.randn(out_dim)
        self.dw = None
        self.db = None
        self.fn = fn[act_fn]
        self.df = df[act_fn]
        self.lr = lr

    def forward(self, x):
        self.x = x
        self.h = np.dot(x, self.W) + self.b
        return self.fn(self.h)
    

    def backward(self, g):
        self.dw = (g * self.df(self.h)).transpose() @ self.x
        self.db = (g * self.df(self.h)).transpose().sum(-1)
        return (g * self.df(self.h)) @ self.W.transpose()

    def update(self, lr=None):
        if lr is not None and self.dw is not None and self.db is not None:
            self.W -= self.dw.transpose() * lr
            self.b -= self.db * lr
            self.dw = None
            self.db = None

class MLP:
    def __init__(self, dims=[1, 5, 5, 1], act='relu', cost='l2'):
        self.layers = []
        self.fn = fn[cost]
        self.df = df[cost]
        for i in range(len(dims)-1):
            act = act if i < len(dims) - 2 else 'none'
            layer = LinearLayer(dims[i], dims[i+1], act)
            self.layers.append(layer)
        
    def forward(self, x):
        for layer in self.layers:
            x = layer.forward(x)
        return x

    def backward(self, g):
        for layer in self.layers[::-1]:
            g = layer.backward(g)

    def update(self, lr):
        for layer in self.layers:
            layer.update(lr)
    
    def loss(self, x, y):
        return self.fn(x, y).mean()
    
    def loss_grad(self, x, y):
        return self.df(x, y)
    

base_lr = 0.1
dims = [1, 10, 10, 1]
N = 500
x = np.linspace(-10, 10, N).reshape(N, 1)
y = np.sin(x) + np.random.randn(N).reshape(N, 1)

nn = MLP(dims)
lr = base_lr / N
losses = []
for epoch in range(10000):
    y_ = nn.forward(x)
    loss = nn.loss(y_, y)
    losses.append(loss)
    grad = nn.loss_grad(y_, y)
    nn.backward(grad)
    nn.update(lr)

plt.figure()
plt.plot(x, y)
plt.plot(x, y_, 'r')

plt.figure()
plt.plot(losses[:100])

plt.show()

我们看到使用ReLU激活函数的MLP拟合的曲面是锯齿状的，这其实非常符合我们的预期：使用若干个linear region的组合来拟合目标曲面。

万能近似定理 Universal Approximation Theorem

早在1989年，该定理就得到了证明:

For any $f:\mathbb{R}^d \to \mathbb{R}^D$ , there exists $f_\epsilon = W_2 \circ \sigma \circ W_1: \mathbb{R}^d \to \mathbb{R}^D$, where $W_1, W_2$ is affine map, $\sigma$ is continous and non-polynomial, such that

$$\sup_{x} || f(x) - f_\epsilon(x) || < \epsilon$$

holds for artitary small $\epsilon$

它说明，我们用有一个隐藏层不限宽度的MLP，就足以逼近任何连续函数。

卷积神经网络 Convolutional Neural Network

如果用MLP处理2D data，比如图像，一般做法是将2D data vectorize成1D，再交给MLP训练。显然这用做法丢弃了原有数据的空间信息(spatial information)，卷积神经网络为此而生。

如下所示，$\circledast$ 代表卷积操作。一个$4\times 4$的输入与一个$3\times3$ 的卷积核的卷积，等价于右边的矩阵相乘的形式，不过我们要将右边的所得的$4 \times 1$ 的结果转回$2\times 2$。事实上早期的深度学习框架Caffe是通过im2col的函数如此操作的。由此可见，卷积本质上也是Linear Operation。

在实践中，$N$张图片数据的格式一般是$N \times H_x \times W_x \times C$ 的4D数据，卷积核一般也会采用$H_y \times W_y \times C \times D$ 的结构，这样卷积会得到一个$N \times H_z \times W_z \times D$ 的结果。记住，卷积操作只是在$H \times W$这两个维度，$C,D$这两个维度就是简单的矩阵相乘。经过几层CNN后，我们将结果vectorise，这样就能丢给后面的MLP处理了。

早期的CNN在MNIST数据集上取得了很不错的成绩。比如上面的LeNet，它用较少的参数量轻松超越了MLP的结果。这表明，人工神经网络有着很大的优化空间。我们在下一节会看到，深度学习的诸多变种都是围绕着卷积进行的。

深度学习 Deep Learning

本次深度学习的引爆，有两个关键因素：数据和算力。互联网时代的到来，为我们提供了海量的数据，特别是图片和视频数据。而这些数据的检索，对算法提出了新的要求。处理这些海量数据，又对计算机的算力提出很高的要求。而摩尔定律又在GPU上得到恰到好处的延续。至此，深度学习的爆发，似乎只是时间问题。

AlexNet

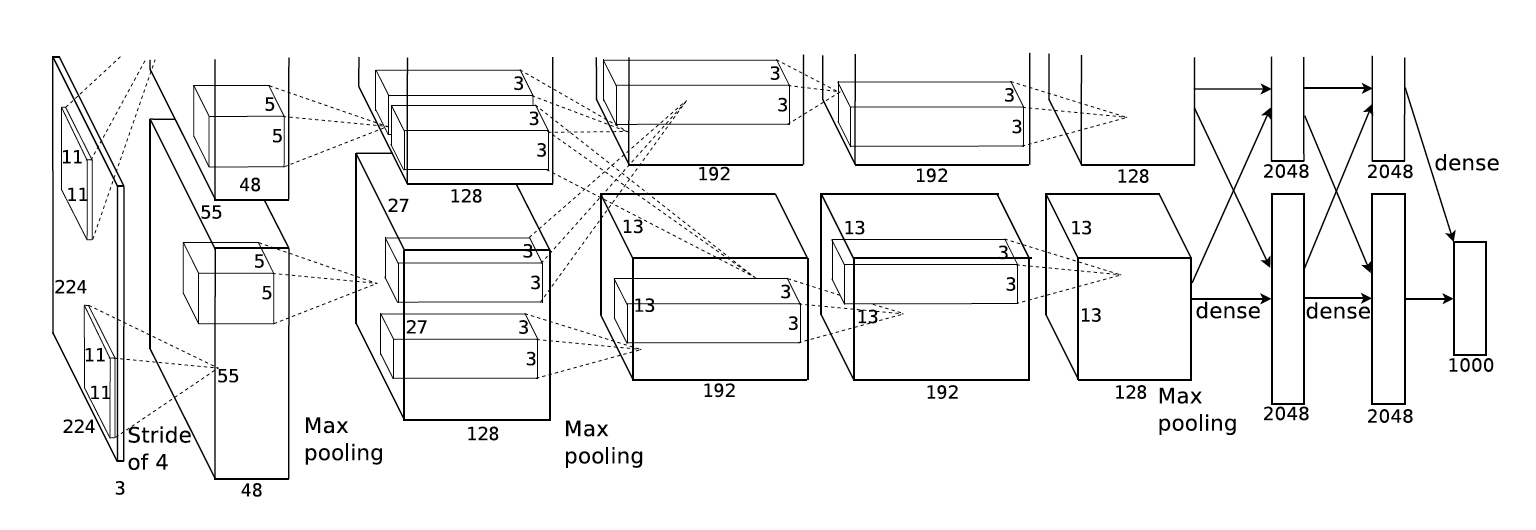
2012年，由Alex Krizhevsk提出的AlexNet参加了当年的ImageNet 大规模视觉识别挑战赛，拿到第一名的夺目成绩，由此拉开了深度学习在视觉竞赛的序幕。以今天的眼光看来，AlexNet相较于LeNet并没有太多改进，无非是扩大了网络的规模。

但是，它开创了本领域很多第一：

1. 第一次用CNN在如此大规模的数据集(1M images, 1000 classes)上取得远超传统算法的成绩。
2. 第一次设计使用如此大规模的神经网络且成功完成训练。
3. 第一次用GPU编程加速训练如此大规模的神经网络，使其训练时间在可接受范围内(5-6 days)。

在不久之后，有人便用了更大更深的网络(VGG)，在同样的数据集下取得了更好的成绩。

ResNet

人们随后发现，简单的增加网络的深度，并不能使结果变得更好，相反结果会变得更差。回看我们在BP中推导出的三层MLP的梯度公式：

我们会发现，在链式法则下，越上层的网络，梯度从底层传导回来经历的计算越多。如果层数变得更多的话，会导致很多问题：

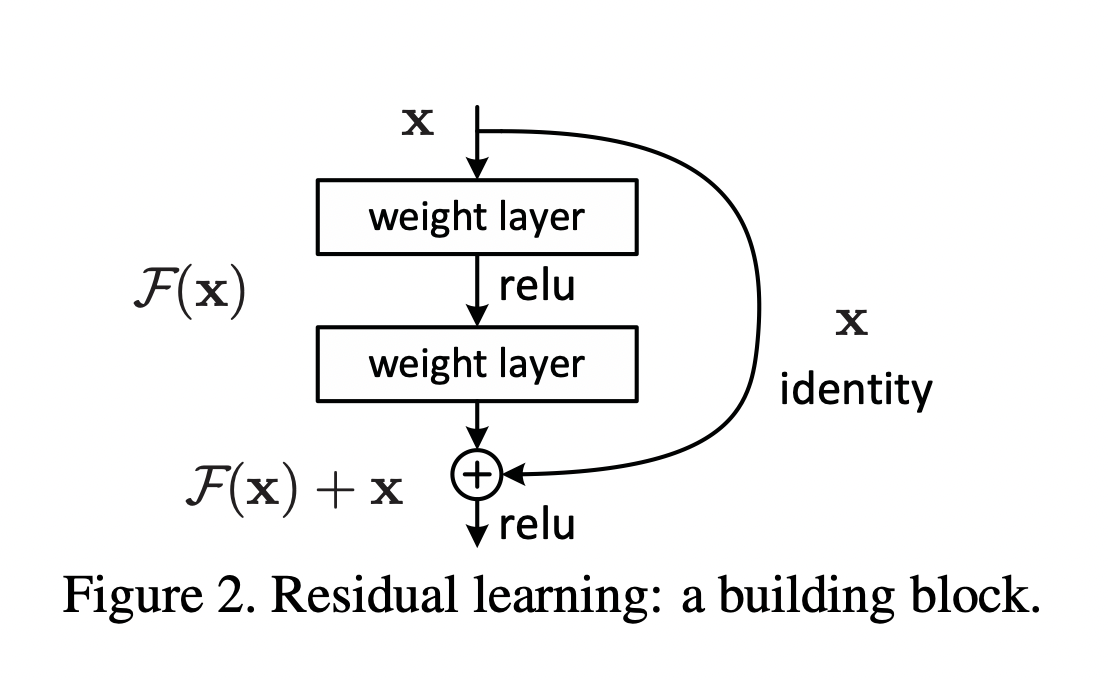
1. 激活函数$ReLU$，其导数$\sigma'(x)$是unit step function，对负数的响应为$0$；层层嵌套后，会导致传回的梯度的很多维度数值为$0$，这就是所谓的梯度消失(vanishing gradient)。
2. 由于我们一般采用随机梯度下降法训练(每次会从数据集中随机取一定数量样本训练)，在计算梯度的过程中，必然会引入噪音(误差)，这些噪音经过层层积累，将会越来越大，从而使得最上层得到的梯度面目全非(被噪音覆盖)。
3. 上层网络的梯度运算中，涉及到下层网络参数$W$的矩阵连乘，所以如果$W$的初始化不好，经过层层叠加，大概率会增大$\sup \|f(Wx+b)\|$，从而使得$\sup \|\partial L/\partial W\|$增加，在更新后会使得$\sup \|W\|$增大，形成恶性循环，这样网络训练几步就会出现数值溢出的错误，这就是所谓的梯度爆炸(exploding gradient)的问题。又因为2中提到的梯度噪音的存在，使得出现梯度爆炸的概率因为网络的变深而大大增加。有兴趣可以我们BP里$W$的初始化改为random normal跑跑看。虽然此问题可以经过较好的参数初始化和梯度裁剪(gradient clip)得到解决，但相比于浅层网络，较深的网络的训练显然会变得不稳定(更容易出现梯度爆炸)。

相信ResNet的作者He Kaiming更能洞悉这些问题。再加上Highway Networks的铺垫，ResNet的提出似乎是顺理成章的事情。ResNet的结构可谓是大道至简：

我们考虑有residual结构的三层MLP：

那么

由上可以看出，在较上层的梯度($\partial L/\partial W_1$)中，因为有Identity Connection的存在，梯度能直接从Loss传回到最上层，从而：

1. 避免因$ReLU$导致的梯度消失。
2. 避免梯度噪音的累积放大。
3. 因为2减少的梯度噪音，梯度爆炸的概率也大大降低了。

在ResNet发布之后，有很多文章对其进行分析。其中有两篇值得一提：

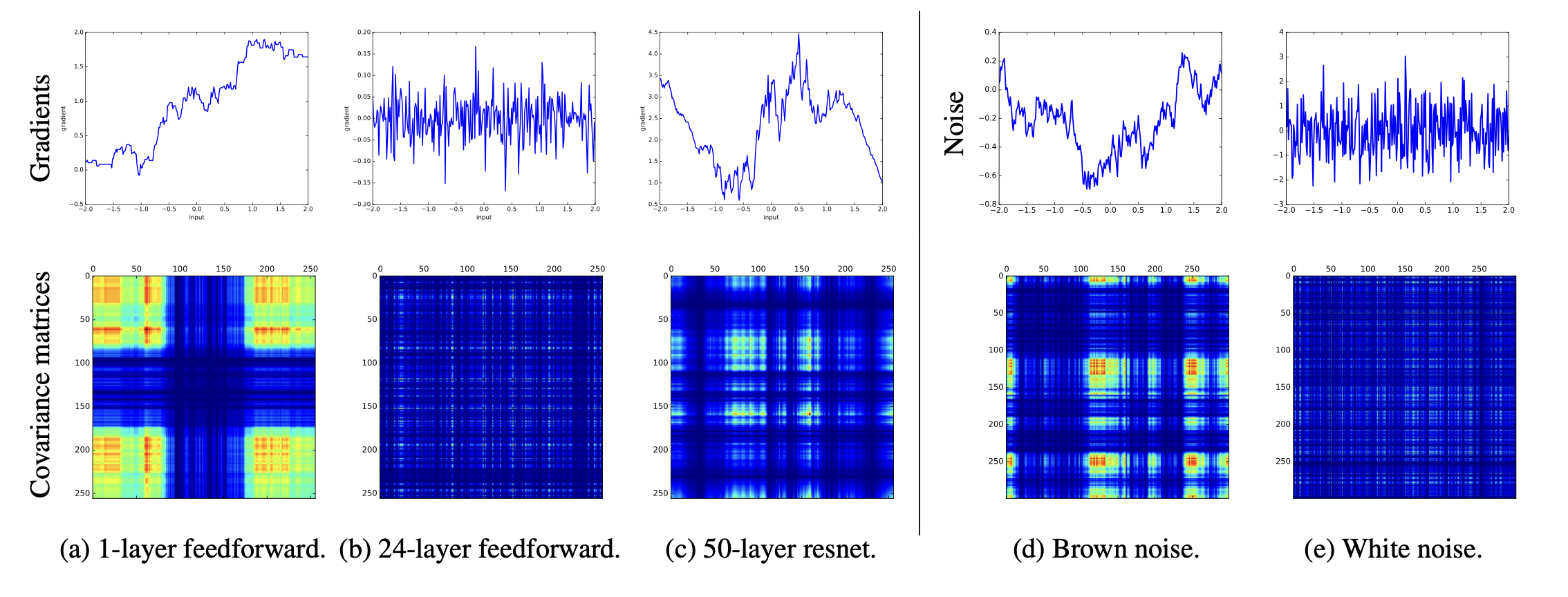
1. The Shattered Gradients Problem: If resnets are the answer, then what is the question?
2. Residual Networks Behave Like Ensembles of Relatively Shallow Networks

第一篇详细的分析了梯度回传中的噪音问题，跟我们的分析非常一致。下图中(d) (e) 列的上行分别代表着采样自brown noise和white noise的数据；下行代表着数据点之间的covariance matrix。(a)(b)(c)的上行是取自单层MLP，24层MLP，和50层有residual结构的MLP的对输入数据(256个数据点取自$[-2,2]$的区间)的梯度；下行是梯度的covariance matrix。我们知道，布朗运动的相邻点之间有很高的相关度，而白噪的数据点之间相关度为0；通过对比我们可以得出结论：如果没有residual结构，回传的梯度间无相关性，接近于白噪；加了residual结构后，回传的梯度间出现了相关性。

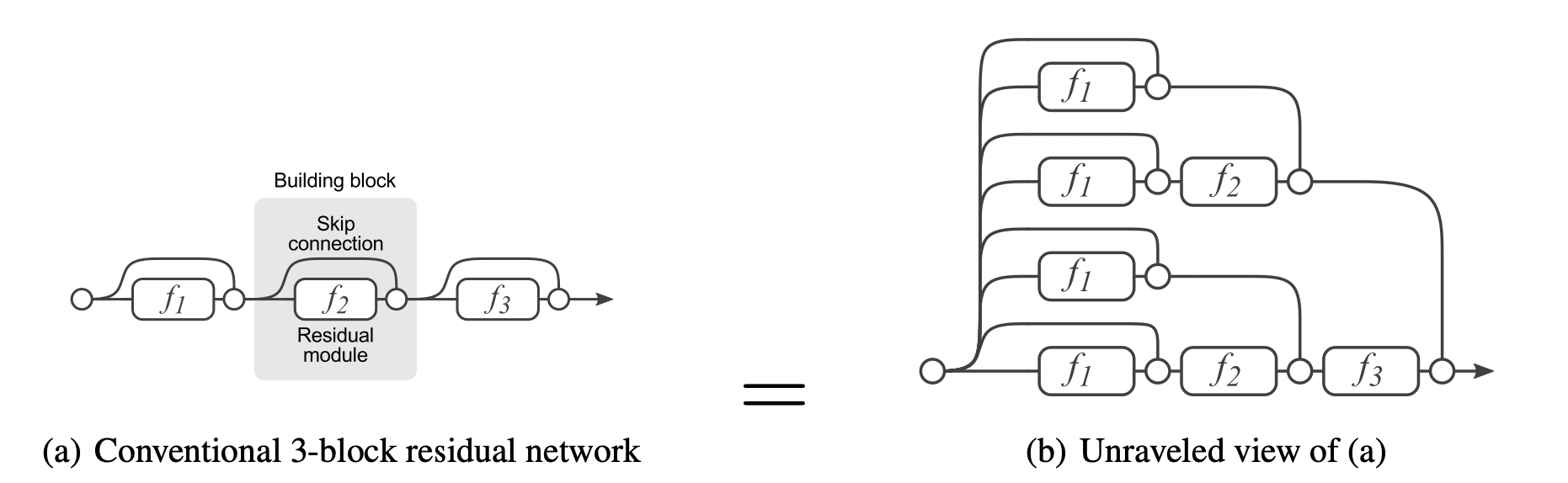
第二篇其实也很直观，一张图足以说明问题：

这也是正是其标题要表达的：

深度残差网络更像是其浅层子网络的集成。

ResNet有很多变种，有将residual block的addition操作改为channel concatenation的DenseNet，有结合两者的DPN，有将channel分组的ResNext，有在channel上加attention的SENet，甚至还有单纯增加网络宽度的WRN(我想说这也好意思单独发出来🐶)，但是ResNet依然是最经典的。

Inception

如果说ResNet代表着大道至简的设计艺术，那么Inception系列更像是精雕细琢的艺术设计。Inception共有四个版本：V1，V2，V3，V4，设计原则都差不多，其中V2提出了Batch Normalization，影响了后来所有神经网络的设计。V4将residual结构加了进来。

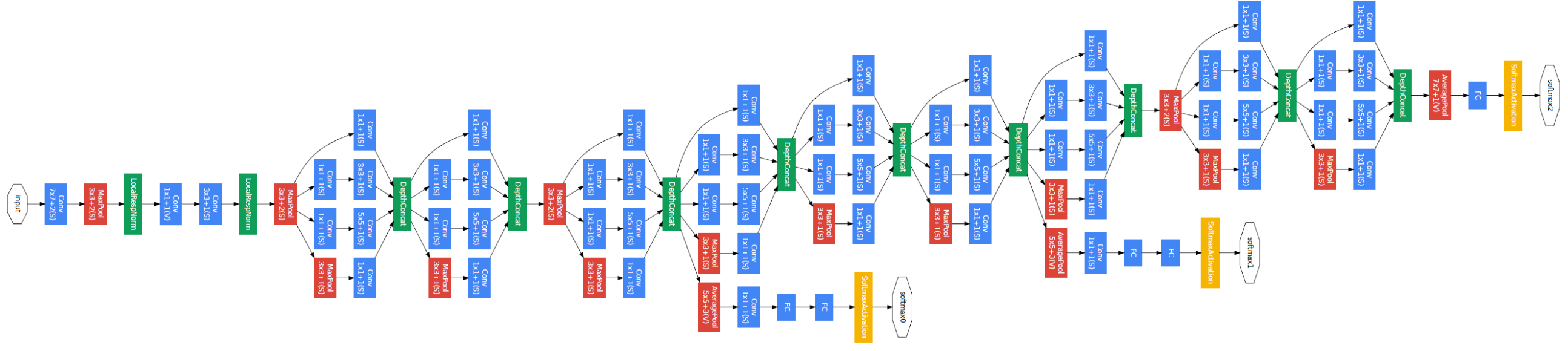
我们只看Inception V1，整个网络看起来是这个样子的：

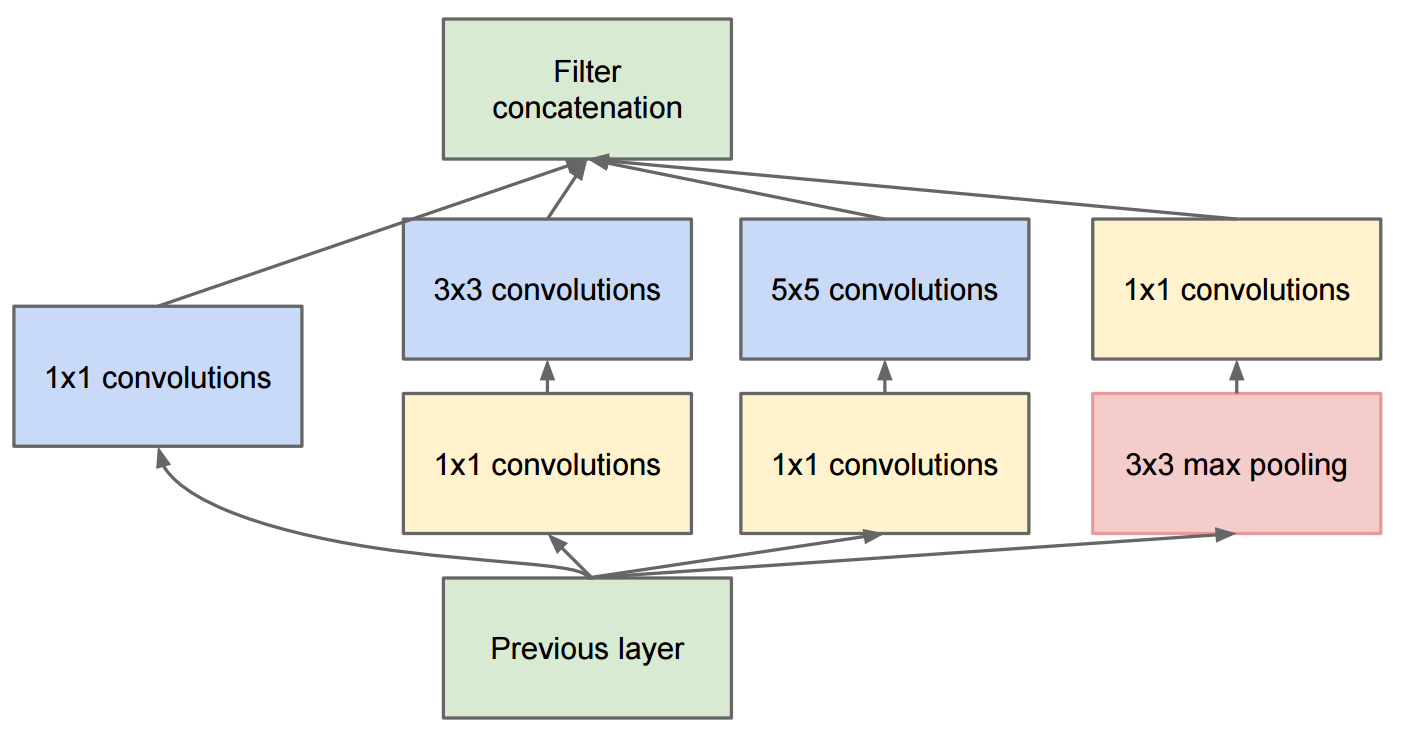
看起来很头疼，但实际上网络是由很多个相似的block叠加，而单个block看起来是下面这样。

我其实很不太理解是什么指导着Google设计出这样复杂的网络，但是大概琢磨着是这样的：

1. 由于众所周知的卷积神经网络的Receptive Field的问题，虽然采用较大的卷积核能减少其负面影响，但带来的新问题是参数量和计算量的指数提升$O(n^2)$，所以我们可以适当中和一下，一部分用小卷积核，一部分用大卷积核，叠加起来看看效果如何。
2. 好像效果还可以，顺着这个思路，我们再增加其他的操作，比如max pooling，比如将$3\times3$的卷积分解成$3 \times 1$和$1 \times 3$ 的卷积叠加，这样又能减少参数和计算量$3 \times 1 + 1 \times 3 = 6 < 3 \times 3 = 9$。
3. 我们依此原则设计几十个这样的网络拿去训练(反正GPU多)，选一个最好的发表出来。

Inception系列网络为google取得了非凡的成绩，也是人工设计网络的巅峰之作，同时，也为机器设计网络提供了灵感。

Neural Architecture Search

上节提到Inception中人工设计的成分，以 Google拥有的海量算力，让机器代替人去设计似乎是一件顺水推舟的事情。以当时该领域的火热程度，有这种想法的不会只有一个人。几乎在同一天，这个想法的两篇文章同时发表:

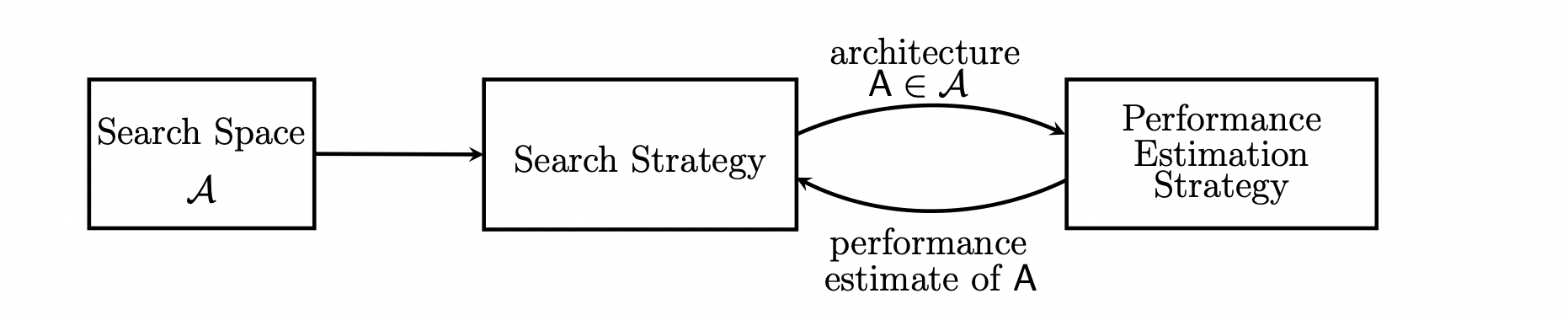
1. Designing Neural Network Architectures using Reinforcement Learning
2. Neural Architecture Search with Reinforcement Learning

相较于Google的资源和影响力，1无论是从结果还是后续上都与2相差甚远，学术界的马太效应非常残酷。两者都试着用reinforcement learning来代替人工设计出更好的网络，设计思想用下图表示：

Search Space

早期的设计是layerwise的，每一个layer给出几个候选的operation，从中sample。后期的设计是blockwise的，就是类似于Inception的block设计，这样就大大减少了搜索空间，提升了搜索效率。

Search Strategy

1. Q Learning: metaQNN，blockQNN
2. Policy Gradient: NASNet
3. Evolution: PNAS
4. Gradient: DARTS
5. Monte Carlo Tree Search
6. Random
7. Bayesian Optimization and others

对于1，2这两种搜索策略，我其实并不看好。一则是reinforcement learning本身学的很慢，消耗如此多的计算资源搜出来的网络，比消耗同样多计算资源随机采样出来的最好的网络，到底有多大提升，本应该打个问号。加上本领域常见的各种trick，使得这种文章的复现变得极为困难。另外，RL最怕的就是reward的随机性，在搜索后期，同一网络准确率的随机性，完全可以覆盖住RL算法想要带来的准确率提升，而RL本身又有很强的随机性。blockQNN用较短的周期训练出来的准确率，代替较长训练周期训练的准确率，则更是在这个问题上火上浇油(因为对于两个较好的网络，通常两者之间的相关性不高)。所以我怀疑，RL做NAS，与其说是在搜较好的网络，不如说在学习如何捕捉到较重的网络(较重和较好正相关，且更容易学到)。这这份怀疑，伴随着NAS101的出现，得到了我的坐实。

至于4，我认为其马太效应会非常明显，因为不同layer之间的相关性得不到体现，相当于RL中没有exploration。这样显然背离了NAS的初衷（因为我们假设不同layer之间是有相关性的)。

至于6，本来应该拿来做baseline的，我在NAS101的实验中发现，其实这个baseline已经很好了，124都很难超越（需要一点运气)，而且即便超越，提升也非常有限。

反观3和5，我认为应该是最合适的搜索策略，但是却最得不到重视。原因是这两个方向没有RL火，学术界么，都喜欢凑热闹。

后NAS时期

我们前面提到，由于搜索策略的低效性，我们通常采用blockwise search来减少搜索空间，然而此举显然会降低搜到的模型的上限。Randomly Wired Network其实提供了另一种思路：在较好的大型搜索空间内，即便网络结构是随机生成的，也会有不错的表现。如果再往下走一步，其实就会更接近生物神经网络的生成模式了。

人的大脑的可塑性非常强。我们一出生，便拥有了一生所需的几乎所有的，且过量的神经元。大约15个月之后，神经元之间的突触连接数便达到最大。这之后，大脑变开始对这些错综复杂的神经连接进行剪枝，直到青春期结束，见这里。而且即便在成年后，大脑也在不断的适应环境，不断的产生新连接和剪枝。

所以，我们能否设计出类似于人脑的学习算法，根据学到的数据，在不同的阶段，不断的更改网络结构呢？

另外，NAS其实属于AutoML的一个分支。训练一个模型，不仅要选择神经网络结构，而且还会需要选择太多的超参数(Hyperparameters, e.g. learning rate, optimizer, data augmentation)，而这些参数的不同排列组合，即便对同一网络，也可能产生残差不齐的结果。不过这，就是另外一个话题了。

平均场论 Mean Field Theory

有关深度学习的理论，个人觉得平均场论的解释非常平易近人。我们简单了解一下。

我们考虑一个hidden layer的MLP: $y = \phi(Wx + b)$，其$W \in \mathbb{R}^{N\times N}$和$b \in \mathbb{R}^{N}$采样自高斯分布:

我们设激活前数值$h = Wx + b$，则其L2 norm的平方:

我们知道，如果$N \ggg 1$，根据中心极限定理(central limit theory)，$h_j$是高斯分布。所以如果我们将网络的输出代入输入作为一个iteration，则有:

如此不断迭代，我们期望得到一个不动点: $q^* = \lim_{t \to \infty}q_t$.

如果输入信号是一对: $x_\alpha, x_\beta$，同理可得:

且我们期望有不动点$\Sigma^* = \lim_{t\to \infty} \Sigma_t$, 则

因为$q_\alpha^* = q_\beta^* = q^*$，我们定义$c^* = q_{\alpha, \beta}^* / q^*$那么

对于不动点$\Sigma^*$，其稳定的条件是$\mathcal{X}_{c^*}<1, \mathcal{X}_{q^*}<1$，对于上述关于$q_t$的动态系统，其Lyapunov Exponent

如此，关于此动态系统的发散与否，只需要确定$\mathcal{X}{c^*}, \mathcal{X}{q^*}$，而这两个数只由$\phi, \sigma_w, \sigma_b$来决定。

对每个不动点的$q^*$，我们设$\mathcal{X}_{q^*} = 1$，则可求出$\sigma_w^2 = 1 / \mathbb{E}[\phi'(h_i)\phi'(h_j)], h_i, h_j \sim \Sigma^*$，从而求出$\sigma_b^2 = q^* - \sigma_w^2$，变化$q^*$的值，则可画出如下$\sigma_w^2 \sim \sigma_b^2$相位图：

我们取$\phi = \tanh$, 摘抄MF的代码如下:

import numpy as np
from scipy.integrate import quad, dblquad
import warnings
import matplotlib.pyplot as plt

def f(x):
    return np.tanh(x)

def df(x):
    """Derivative of tanh."""
    return 1. / np.cosh(x)**2

def gauss_density(x, mu, sigma):
    """Density of Gaussian N(mu,sigma)."""
    k = 1. / (sigma * np.sqrt(2 * np.pi))
    s = -1.0 / (2 * sigma * sigma)
    return k * np.exp(s * (x - mu) * (x - mu))

def qmap_density(h, q):
    """Compute the density function of the q-map."""
    return gauss_density(h, 0., np.sqrt(q)) * (f(h)**2)

def chi_c1_density(h, q):
    """Compute the density function of chi_c=1."""
    return gauss_density(h, 0., np.sqrt(q)) * (df(h)**2)

def sw_sb(q, chi1):
    """
    Compute the critical line. Set chi1=1, return variances of weight and
    bias on the critical line with qstar=q.
    """
    with warnings.catch_warnings():
        # silence underflow and overflow warning
        warnings.simplefilter("ignore")
        sw = chi1 / quad(chi_c1_density, -np.inf, np.inf, args=(q))[0]
        sb = q - sw * quad(qmap_density, -np.inf, np.inf,
                            args=(q))[0]
    return sw, sb

def simple_plot(x, y):
    plt.plot(x, y)
    plt.xlim(0.5, 3)
    plt.ylim(0, 0.25)
    plt.xlabel('$\sigma_\omega^2$', fontsize=16)
    plt.ylabel('$\sigma_b^2$', fontsize=16)
    plt.show()

def main():
    qrange = np.linspace(1e-5, 2.25, 50)
    sw_sbs = [sw_sb(q, 1.0) for q in qrange]
    sw = [sw_sb[0] for sw_sb in sw_sbs]
    sb = [sw_sb[1] for sw_sb in sw_sbs]

    simple_plot(sw, sb)

main()

同理，我们固定$\sigma_b^2=0.05$和，变化$\sigma_w^2$，从而求出$\mathcal{X}_{q^*}$与$q^*$，也可画出$\sigma_w^2 \sim t \sim |q_t - q^*|$的关系图（下图中白色断线），我们发现此图的与我们据此参数训练出的网络的准确率惊人一致，特别的，当$\sigma_w^2 = 1.75$时候，$\mathcal{X}_{q^*} = 1, \xi_{q^*}^{-1}=0$，而$|q_t - q| = k_q$，此时，理论上模型允许成功训练的深度最大，而这也在下图中得到了体现。

总之，平均场论主要回答了一下问题：神经网络参数的初始化，是如何影响模型的收敛性的？其理论推论与实验高度吻合，可以说是深度学习理论里，少有的干得漂亮的作品。