一、基础 Foundations

1.1 介绍

简单介绍何为算法，它能解决什么样的问题，介绍NP完全问题。

1.2 算法复杂度

\log{n} < \sqrt{n} < n < n \log{n} < n^2 < n^3 < 2^n < n! \quad \text{when} \quad n \rightarrow \infty

二、基本算法 Basic Algorithms

2.1 Insert Sort $O(n^2)$

def insert_sort(A, reverse=False):
    for j in range(1, len(A)):
        key = A[j]
        i = j - 1

        # Insert A[j] to sorted sequence of A[:j]
        if reverse:
            while i >= 0 and A[i] < key:
                A[i+1] = A[i]
                i -= 1
        else:
            while i >= 0 and A[i] > key:
                A[i+1] = A[i]
                i -= 1
        A[i+1] = key

    return A

2.3 Merge Sort $O(n\log n)$

def merge(A, p, q, r):
    L = A[p:q] + [float('inf')]
    R = A[q:r] + [float('inf')]

    i, j = 0, 0
    for k in range(p, r):
        if L[i] <= R[j]:
            A[k] = L[i]
            i += 1
        else:
            A[k] = R[j]
            j += 1

def merge_sort(A, p, r):
    if p < r:
        q = int((p + r) / 2)
        if q == p:
            merge(A, p, p+1, r+1)
        else:
            merge_sort(A, p, q)
            merge_sort(A, q, r)
            merge(A, p, q, r)
    return A

三、算法复杂度 Algorithm Complexity

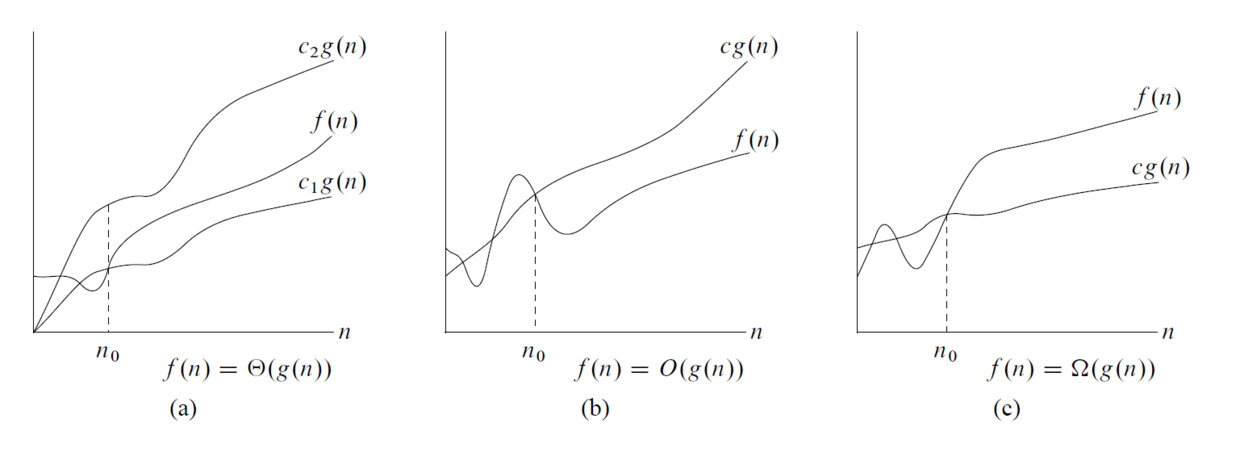
We say an algorithm's complexity is $O(n^2)$ means:

There exists $c > 0, n_0 > 0$ such that running time of the algorithm is below $c n^2$ when $n > n_0$

四、分而治之 Divide and Conquer

4.1 Find maximum subarray

An array has $n(n+1)$ subarrays, find the maximum sum of all the subarrays.

def find_maximum_cross_subarray(A, low, mid, high):
    left_sum = - float('inf')
    sum_ = 0
    for i in range(mid, low-1, -1):
        sum_ += A[i]
        if sum_ > left_sum:
            left_sum = sum_
            max_left = i
    
    right_sum = - float('inf')
    sum_ = 0
    for j in range(mid+1, high+1):
        sum_ += A[j]
        if sum_ > right_sum:
            right_sum = sum_
            max_right = j
    
    return max_left, max_right, left_sum + right_sum

def find_maximum_subarray(A, low, high):
    if high == low:
        return low, high, A[low]
    
    else:
        mid = (low + high) // 2
        left_low, left_high, left_sum = find_maximum_subarray(A, low, mid)
        right_low, right_high, right_sum = find_maximum_subarray(A, mid+1, high)
        cross_low, cross_high, cross_sum = find_maximum_cross_subarray(A, low, mid, high)
    
    if left_sum >= right_sum and left_sum >= cross_sum:
        return left_low, left_high, left_sum
    elif right_sum >= left_sum and right_sum >= cross_sum:
        return right_low, right_high, right_sum
    else:
        return cross_low, cross_high, cross_sum

六、堆排序 Heap Sort

Heap (tree) has following properties:
Parent of node $i$ is node $[i/2]$
Right child of node $i$ is node $2i+1$
Left child of node $i$ is node $2i$

A max-heap is such that the value of node ii is smaller than its parent node's value.

def max_heapify(A, i, till):
    l = 2*i
    r = 2*i + 1

    if l < till and A[l] < A[i]:
        largest = l
    else:
        largest = i
    
    if r < till and A[r] < A[largest]:
        largest = r
    
    if largest != i:
        A[i], A[largest] = A[largest], A[i]
        max_heapify(A, largest, till)

    return A

def heap_sort(A):
    for i in range(len(A) // 2, -1, -1):
        max_heapify(A, i, len(A))
    print(A)
    for i in range(len(A)-1, 0, -1):
        A[0], A[i] = A[i], A[0]
        A = max_heapify(A, 0, i)
    return A

七、快排序 Quick Sort

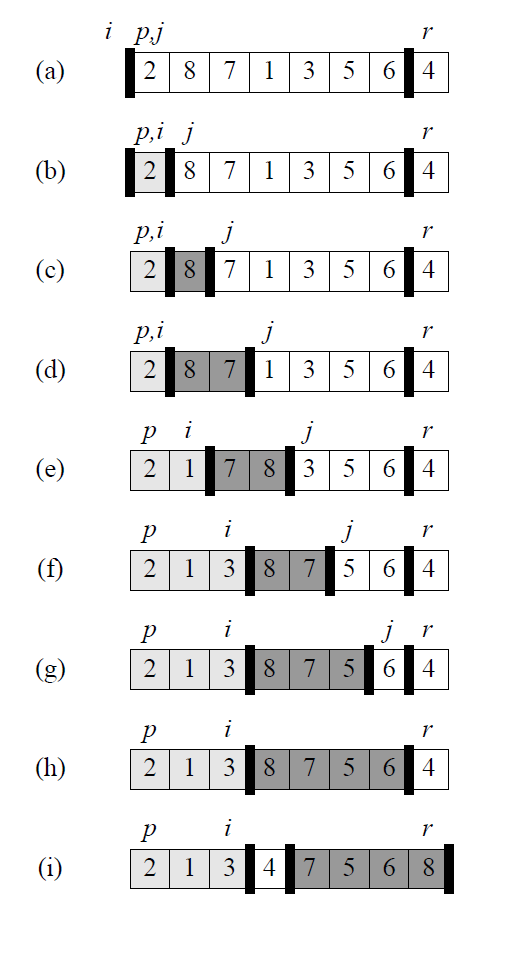
def partition(A, p, r):
    x = A[r]
    i = p - 1
    for j in range(p, r):
        if A[j] <= x:
            i += 1
            A[i], A[j] = A[j], A[i]
    A[i+1], A[r] = A[r], A[i+1]
    return i+1

def quick_sort(A, p, r):
    if p < r:
        q = partition(A, p, r)
        print(p, q, r, A)
        quick_sort(A, p, q-1)
        quick_sort(A, q+1, r)

十、数据结构 Data Structure

Queue: First In First Out
Stack: First In Last Out
LinkedList:

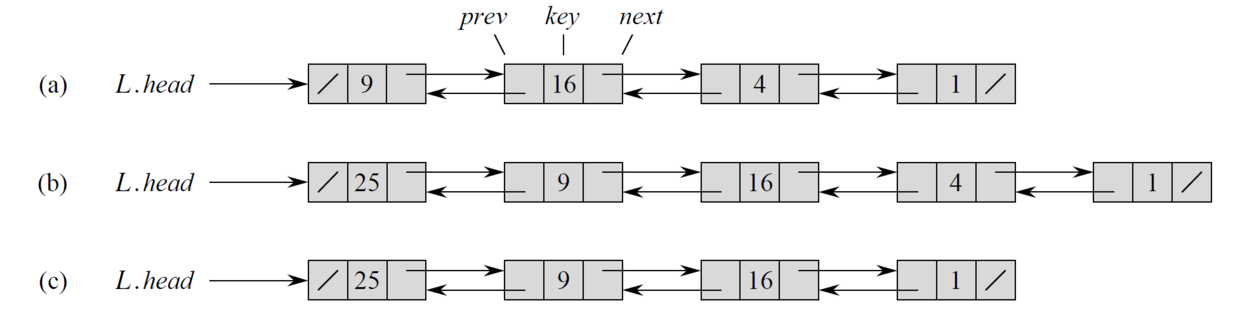
十一、哈希表 Hash Table

十二、二叉树 Binary Tree

Let $x$ be a node in a binary search tree. If $y$ is a node in the left subtree of $x$ , then $y.key < x.key$ ; if $y$ is a node in the right subtree of $x$ , then $y.key >= x.key$

class Node:
    def __init__(self, left=None, right=None, parent=None, key=None):
        self.left = left
        self.right = right
        self.parent = parent
        self.key = key

def in_order_tree_walk(x:Node):
    if x != None:
        in_order_tree_walk(x.left)
        print(x.key)
        in_order_tree_walk(x.right)

def tree_search(x, k):
    if x == None or k == x.key:
        return x
    if k < x.key:
        return tree_search(x.left, k)
    if k > x.key:
        return tree_search(x.right, k)

def iterative_tree_search(x, k):
    while x is not None and k != x.key:
        if k < x.key:
            x = x.left
        else:
            x = x.right
    return x

def tree_min(x):
    while x.left is not None:
        x = x.left
    return x

def tree_max(x):
    while x.right is not None:
        x = x.right
    return x

def tree_succ(x):
    if x.right is not None:
        return tree_min(x.right)
    
    y = x.parent
    while y is not None and x == y.right:
        x = y
        y = y.parent
    return y

def tree_prec(x):
    if x.left is not None:
        return tree_max(x.left)
    
    y = x.parent
    while y is not None and x == y.left:
        x = y
        y = y.parent
    return y

Introduction to Algorithms 下载地址:

Introduction_to_algorithms-3rd%20Edition.pdf