论文笔记 Approximately Optimal Approximate Reinforcement Learning

这篇提出一种Conservative Policy Iteration algorithm，可以在较小步数内，找到近似最优策略(Approximately Optimal Policy)，这也是知名的Trust Region Policy Optimisation的前作。

文章第二部分给出一些RL的基本定义：

V_\pi(s) = (1 - \gamma)E_{s,a}[\sum_{t=0}^{\infty} \gamma^t R(s_t,a_t) | \pi, s] \\Q_\pi(s,a) = (1 - \gamma)R(s,a) + \gamma E_{s'}[V_\pi(s')|\pi,s]

这里加 $1-\gamma$ 是为了让 $V_\pi(s), Q_\pi(s,a) \in [0, R_{\max}]$ ，因为

E_{s,a}[\sum_{t=0}^{\infty} \gamma^tR(s,a)|\pi] \leq R_{\max} + \gamma R_{\max} + \dots = R_{\max} / (1 - \gamma)

这样advantage function

A_\pi(s,a) = Q_\pi(s,a) - V_\pi(s,a) \in [-R_{\max}, R_{\max}]

还给出了一个 discounted future state distribution 的定义

d_{\pi, D} = (1 - \gamma) \sum_{t=0}^{\infty} \gamma^t Pr(s_t = t | \pi, D)

这样，给定一个 start state distribution $D$ , policy optimization 的目标函数

\eta_D (\pi) = E_{s \sim D} [V_\pi(s)] = E_{s,a \sim d_\pi, \pi} [R(s,a)]

我们展开的话，会发现:

\tau = (s_0, a_0, s_1, a_1, \dots),\quad s_0 \sim D, \quad a_t \sim \pi(s_t),\quad s_{t+1} \sim Pr(s'|s=s_t, a=a_t)\\ Pr(\tau) = D(s_0) \prod_{t=0}^{\infty} \pi(s_t,a_t)Pr(s_{t+1}|s_t, a_t)\\R(\tau) = (1-\gamma)\sum_{t=0}^{\infty}\gamma^tR(s_t,a_t) \\\eta(\pi) = E_{\tau}[R(\tau)]

由上很容易推出：

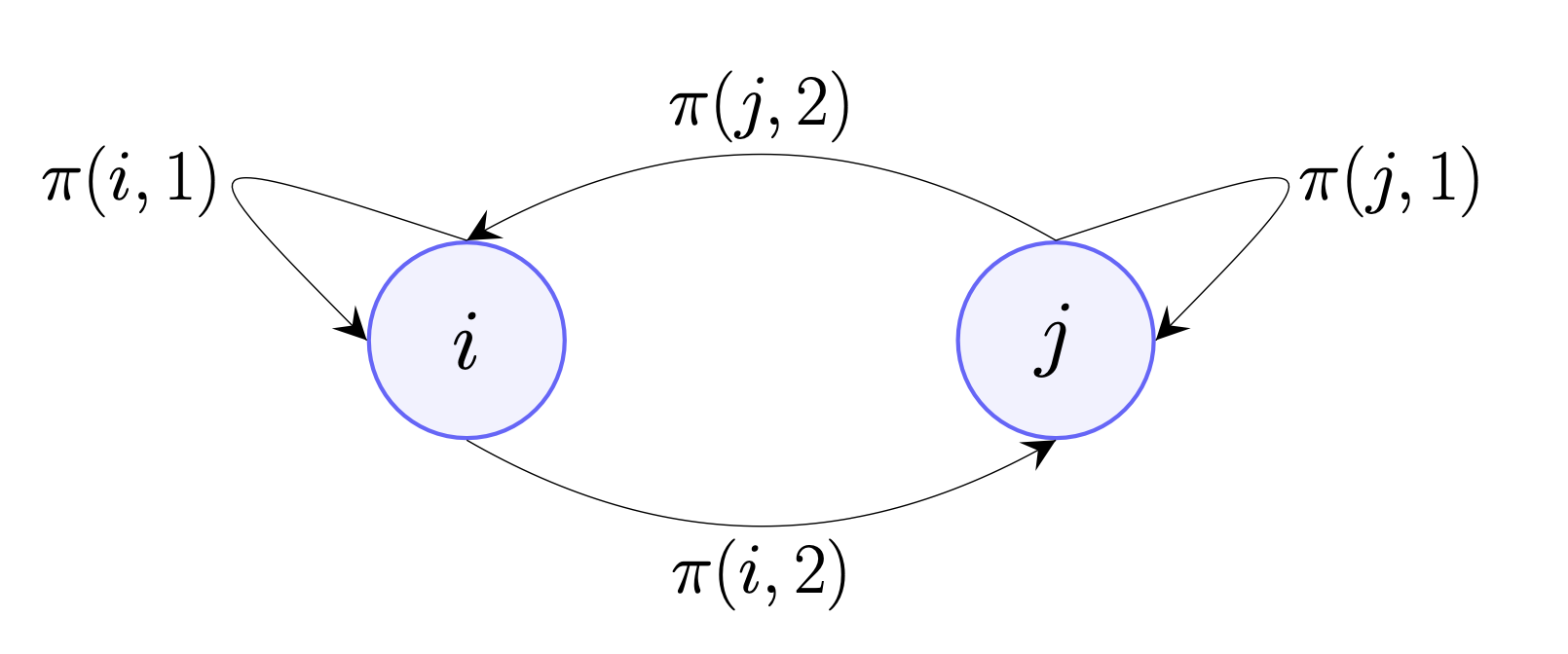
\eta (\pi) = \sum_{s}d_{\pi,D}(s)\sum_{a}\pi(s,a)Q(s,a)

文章第三部分，主要提出policy optimization 面临的两大难题，Figure 3.1 是sparse reward的问题；Figure 3.2是flat plateau gradient的问题。我们讨论Figure 3.2的case。

该图所示MDP有 $i,j$ 两个states, initial state distribution 为 $p$ ，initial policy为 $\pi$ ，具体如下

p(i) = 0.8, p(j) = 0.2 \\ \pi(i,1) = 0.8, \pi(i,2) = 0.2 \\ \pi(j,1) = 0.9, \pi(j,2) = 0.1 \\ R(i,1) = 1, R(j,1) = 2, R(i,2) = R(j,2) = 0

很显然， state $j$ 的self loop为最优解。

我们考虑一个parameterized policy function

\pi_\theta(s,a), \quad \pi(a|s) = \frac{e^{\theta_s}}{\sum e^{\theta_s}}, \quad \theta \in \mathbb{R}^{|S| \times |A|}

对应到此MDP， $\theta$ 是 $2 \times 2$ 的矩阵，对目标函数求导:

\nabla_\theta \eta(\pi) = \sum_{s,a} d(s) \nabla\pi(s,a)Q_\pi(s,a)

我们这里肯定是希望增加 $\theta_{i,2}, \theta_{j,1}$ ，然而：

\nabla_{\theta_{i,2}} \eta = d(i) Q(i,2)\pi(i,2)(1-\pi(i,2)) - d(i) Q(i ,1) \pi(i, 1)\pi(i,2) \\ \nabla_{\theta_{j,1}} \eta = d(j) Q(j,1)\pi(j,1)(1-\pi(j,1)) - d(j) Q(j ,2) \pi(j, 1)\pi(j,2)

第一项， $Q(i, 1) \gg Q(i,2)$ ，第二项，因为 $d(j) \ll d(i)$ ，

这样，policy gradient 非常小，学的就太慢了。本文就是为了解决这种问题而生。

文章考虑以下混合策略：

\pi_{new} = (1 - \alpha) \pi + \alpha \pi', \alpha \in [0, 1] \\\pi' = \pi + \nabla \pi

我们记policy advantage：

A_\pi(\pi') = \sum_s d(s,\pi) \sum_a \pi'(s,a) A(s,a)

给出引理一如下：

Lemma 1.
$\eta(\pi_{new}) - \eta(\pi) \geq \alpha A_\pi(\pi') - \frac{2\alpha^2\gamma\epsilon}{1 - \gamma(1-\alpha)} \\ \epsilon = \frac{1}{1-\gamma} \max_s \sum_a \pi'(s,a) A_\pi(s,a)$

证明以上引理，首先，

\begin{aligned} \nabla_\alpha \eta (\pi_{new}) &= \sum_s d(s, \pi_{new}) \sum_a ((1 - \alpha) \pi + \alpha \pi') Q^{\pi_{new}} \\ &= \sum_s d(s, \pi_{new}) \sum_a (\pi' - \pi) (V^{\pi_{new}} + A^{\pi_{new}}) \end{aligned}

那么当 $\alpha \to 0, \pi_{new} \to \pi$ ,

\begin{aligned} \nabla \eta_\alpha (\pi_{new}) |_{\alpha=0} &= \sum_s d(s,\pi) \sum_a (V^\pi + A^\pi)(\pi' - \pi) \\ &= \sum_s d(s,\pi) V^\pi \sum_a (\pi' - \pi) + \sum_s d(s,\pi) \sum_a A^\pi(\pi' - \pi) \\ &= \sum_s d(s,\pi) \sum_a A^\pi(\pi' - \pi) \\ &= \sum_s d(s,\pi) \sum_a A^\pi\pi' \\ &= A_\pi(\pi') \end{aligned}\\

以上倒数第二，三是因为：

\sum_a (\pi - \pi') = \sum_a \pi - \sum_a \pi' = 1 - 1 = 0 \\ \begin{aligned} \sum_s d(s, \pi) \sum_a A^\pi\pi &= \sum_s d(s,\pi) \sum_a (Q^\pi - V^\pi)\pi \\ &= \sum_s d(s,\pi) \sum_a \pi Q^\pi - \sum_s d(s,\pi) V^\pi \sum_a \pi \\ &= \eta(\pi) - \eta(\pi) \\ &= 0 \end{aligned}

根据泰勒展开：

\eta(\pi_{new}) = \eta(\pi) + \alpha \nabla_\alpha \eta(\pi_{new}) + O(\alpha^2)

那么

\eta(\pi_{new}) - \eta(\pi) = \alpha A_\pi(\pi') + O(\alpha^2)

先hold一下，我们给出引理二：

Lemma 2.
$\eta(\hat\pi) - \eta(\pi) = \sum_s d(s, \hat\pi) \sum_a \hat\pi(s,a) A^\pi(s,a)$

证明：

\begin{aligned} \eta(\hat\pi|s_1) &= V^{\hat\pi}(s_1) \\ &= E_{s, a \sim \hat\pi} [\sum_{t=1}^\infty \gamma^{t-1}R(s_t, a_t)|s_1] \\ &= \sum_{t=1}^{\infty} \gamma^{t-1} E_{s,a \sim \hat\pi}[R(s_t, a_t) + V^\pi(s_t) - V^\pi(s_t) | s_1] \\ &= \sum_{t=1}^{\infty} \gamma^{t-1} E_{s,a \sim \hat{\pi}}[R(s_t, a_t) + \gamma V^\pi(s_{t+1}) - V^\pi(s_t) | s_1 ] + V^\pi(s_1) \\ &=\sum_{t=1}^{\infty} \gamma^{t-1} E_{s,a \sim \hat\pi}[Q^\pi(s_t, a_t) - V^\pi(s_t) | s_1 ] + V^\pi(s_1) \\ &= \sum_{s} d(s, s_1, \hat\pi)\sum_a \hat\pi(s,a)A^\pi(s,a) + V^\pi(s_1) \end{aligned}

倒数第三步是因为：

\begin{aligned} & \sum_{t=1}^{\infty} \gamma^{t-1} E_{s,a \sim \hat\pi}[ \gamma V^\pi(s_{t+1}) | s_1 ] + V^\pi(s_1) \\ =& E_{s,a \sim \hat\pi}[ V^\pi(s_1) + \gamma V^\pi(s_2) + \gamma^2 V^\pi(s_3) + \dots | s_1] \\ =& \sum_{t=1}^{\infty} \gamma^{t-1} E_{s,a \sim \hat\pi}[V^\pi(s_t)|s_1] \end{aligned}

因为initial state distribution 相等，所以

\eta(\hat\pi) = \sum_s d(s, \hat\pi) \sum_a \hat\pi(s,a) A^\pi(s,a) + \eta(\pi) \\\eta(\hat\pi) - \eta(\pi) = \sum_s d(s, \hat\pi) \sum_a \hat\pi(s,a) A^\pi(s,a)

引理二证毕。我们回过头继续证明引理一，对比下发现：

\begin{aligned} \eta(\pi_{new}) - \eta(\pi) &= \alpha A_\pi(\pi') + O(\alpha^2) \\ \eta(\pi_{new}) - \eta(\pi) &= \sum_s d(s, \pi_{new}) \sum_a \pi_{new}(s,a) A^\pi(s,a) \end{aligned}

据此提示，我们来求余项：

\begin{aligned} \eta(\pi_{new}) - \eta(\pi) &= \sum_s d(s, \pi_{new}) \sum_a \pi_{new}(s,a) A^\pi(s,a) \\ &= E_{s \sim \pi_{new}}[\sum_t \gamma^{t-1} \sum_a \pi_{new}A^\pi] \\ &= E_{s \sim \pi_{new}}[\sum_t \gamma^{t-1} \sum_a \alpha \pi' A^\pi] \end{aligned}

这里还是用了 $\sum_a \pi A^\pi = 0$ 的性质。接下来我们这么想， $\pi_{new} \sim (\pi(s,a), \pi'(s,a))$ with probability $(1- \alpha, \alpha)$ ,那么，在前 $t$ 步一直取 $\pi_{new} = \pi$ 的概率为 $1 - p_t = (1-\alpha)^t$ ，那么 $p_t = 1 - (1 - \alpha)^t$ ，我们记前 $t$ 步取 $\pi(s,a)$ 的次数为 $n_t$ , 那么 $n_t = 0$ 意味着在前 $t$ 步 $\pi_{new} = \pi$ ，所以

\begin{aligned} & \eta(\pi_{new}) - \eta(\pi) \\ =& E_{s \sim \pi_{new}}[\sum_t \gamma^{t-1} \sum_a \alpha \pi' A^\pi] \\ =& \alpha\sum_t (1-p_t) \gamma^{t-1} E_{s\sim\pi_{new}}[\sum_a \pi'A^\pi | n_t = 0] + \alpha \sum_t p_t \gamma^{t-1} E_{s\sim \pi_{new}}[\sum_a \pi'A^\pi | n_t > 0] \\ =& \alpha \sum_t (1 - p_t) \gamma^{t-1} E_{s\sim \pi}[\sum_a \pi'A^\pi|n_t=0]+ \alpha \sum_t p_t \gamma^{t-1} E_{s\sim \pi_{new}}[\sum_a \pi'A^\pi | n_t > 0] \\ =& \alpha \sum_t \gamma^{t-1} E_{s\sim \pi}[\sum_a \pi'A^\pi] - \alpha\sum_t p_t \gamma^{t-1}E_{s\sim\pi}[\sum_a \pi'A^\pi|n_t=0] + \alpha\sum_t p_t \gamma^{t-1}E_{s\sim\pi_{new}}[\sum_a \pi'A^\pi|n_t>0] \\ =& \alpha A_\pi(\pi') - \alpha\sum_t p_t \gamma^{t-1}E_{s\sim\pi}[\sum_a \pi'A^\pi|n_t=0] + \alpha\sum_t p_t \gamma^{t-1}E_{s\sim\pi_{new}}[\sum_a \pi'A^\pi|n_t>0] \\ \geq& \alpha A_\pi(\pi') - 2 \alpha \sum_t p_{t-1} \gamma^{t-1} \max_s \sum_a \pi'A^\pi \\ =& \alpha A_\pi(\pi') - 2 \alpha \epsilon(1-\gamma) \sum_t(1 - (1 - \alpha)^{t-1})\gamma^{t-1} \\ =& \alpha A_\pi(\pi') - 2\alpha\epsilon(1-\gamma)(\frac{1}{1-\gamma} - \frac{1}{1 - (1-\alpha)\gamma}) \\ =& \alpha A_\pi(\pi') - 2\alpha\epsilon\frac{\alpha\gamma}{1-(1-\alpha)\gamma} \\ \geq & \alpha A_\pi(\pi') - \frac{2\alpha^2\epsilon}{1-\gamma} \end{aligned}\\

这里 $\max_s \sum_a \pi'A^\pi = \epsilon (1-\gamma)$ ，那么

\eta(\pi_{new}) - \eta(\pi) \geq \alpha A_\pi(\pi') - 2\alpha\epsilon\frac{\alpha\gamma}{1-(1-\alpha)\gamma}

至此，引理一证毕。

回过头看，引理一说明了什么？它说明，如果我们用这种混合策略，那么我们就能保证了策略效果提升的下界。有了以上引理，我们接下来确定混合策略的参数 $\alpha$ 。

我么知道

\epsilon =\frac{ \max_s \sum_a \pi'A^\pi }{1-\gamma}\leq R/(1-\gamma)

那么

\alpha A_\pi(\pi') - \frac{2\alpha^2 \epsilon}{1 - \gamma} \geq 0 \Rightarrow \alpha \leq (1-\gamma)^2 A_\pi(\pi') / 2R

我们取

\alpha = (1-\gamma)^2 A_\pi(\pi') / 4R

即可确保

\eta(\pi_{new}) - \eta(\pi) \geq \frac{ A_\pi (\pi')^2(1-\gamma)^2}{8R}

好了，有了以上理论基础，我们来看看作者提出的算法。假设我们有一个advantage function approximator

\hat A^\pi(s,a) \approx A^\pi(s,a)

我们设

\hat A = \sum_s d(s, \pi) \max_a \hat A(s,a)

即可确保

(1-\gamma) \hat A \geq (1-\gamma) \max_{\pi'} A_\pi(\pi') - \delta/3

如何确保？我们用NN来做advantage function approximator

f_w(s,a) = \hat A^\pi

(1-\gamma)\sum_s d^\pi(s) \max_a |A^\pi(s,a) - f_w(s,a)|

以上loss可通过 $\pi$ 的采样获得，需要至少轨迹数为

\frac{R^2} {\epsilon^2} \log \frac{R^2} {\epsilon^2}

如果 $(1-\gamma)\hat A \leq 2\delta/3$ 则停止更新策略，否则：

\pi \leftarrow (1-\alpha)\pi + \alpha \pi' \\\pi' = \arg\max_a f_w(s,a) \\ \alpha = (\hat A - \frac{\delta}{3(1-\gamma)})\frac{(1-\gamma)^2}{4R}

那么以上算法，可确保 $(1 - \gamma) \hat A \geq 2\delta/3$ ，从而

A_\pi(\pi') = \hat A - \frac{\delta}{3(1-\gamma)} \geq \frac{\delta}{3(1-\gamma)}

因此

\eta(\pi_{new}) - \eta(\pi) \geq \frac{ A_\pi(\pi')^2 (1-\gamma)^2 }{8R} \geq \frac{\delta^2}{9(1-\gamma)^2} \frac{(1-\gamma)^2}{8R} = \frac{\delta^2}{72R}

因为对于任意 $\pi:\eta(\pi) \leq R/(1-\gamma)$ ，所以我们最多需要

\frac{R}{1-\gamma} \frac{72R}{\delta^2}

使得

\max_a' A_\pi(\pi') \leq \delta

总结算法如下：

初始化 $f_w(s,a)$ ，随机策略 $\pi$ ，确定 $\delta, \gamma$
求出 $\hat A = \max_a f_w(s,a)$ ，用 $\pi$ 采样，计算 $A_\pi(s,a)$ ，更新 $f_w$
如果 $(1-\gamma)\hat A \leq 2\delta/3$ ，结束算法，返回策略 $\pi$
否则 $\pi' = \arg\max_a f_w(s,a);\pi \leftarrow (1-\alpha)\pi + \alpha \pi'$ ，回到第二步

以上就是Approximately Optimal Approximate RL的内容。